QUELQUES RAPPELS UTILES
Sens de l'écriture
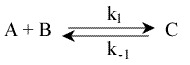
Cette façon d'écrire signifie que la réaction où A donne B, se fait selon une certaine vitesse qui dépend uniquement de la concentration en A, composé qui se trouve du côté de l'empennage de la flèche. La concentration en B n'intervient pas du tout dans la vitesse de la réaction. Si, de fait, elle intervenait, alors on devrait écrire :
En effet, les composés A et B apparaissent chacun du côté de l'empennage d'une des flèches, ce qui est la façon de signaler que leur concentration instantanée influence la vitesse de la réaction. Notez que, dans le cas de la réaction :
la réaction ne met en jeu que le composé A qui se transforme en B, sans l'intervention d'aucun autre réactif et sans intermédiaire.
Prenons le cas d'une réaction hypothétique du type :
et 
Ici, le bilan global est encore , mais la vitesse de la réaction dépend des concentrations instantanées de A, C et E. et pas de la concentration de A seulement.
Il faut donc bien faire la différence entre un schéma cinétique comme celui de l'en-tête qui sert à représenter la réalité de la réaction et le bilan d'un ensemble de réaction, bien qu'on les écrits parfois de la même façon. Par exemple, le bilan de la glycolyse, qui est :
D-glucose + 2Pi + 2ADP + 2NAD+
2pyruvate + 2NADH + 2H+ + 2ATP + 2H2O
ne dit rien sur la vitesse de l'ensemble de la transformation qui passe par de nombreuses étapes.
Ordre de réaction et constante de vitesse
Réaction d'ordre 0 apparent
Dans ce cas, la vitesse est constante et ne dépend pas de la concentration en réactant : v = k
et la constante de vitesse, k, s'exprimera en M T-1
Réaction d'ordre 1 apparent
Dans ce cas, la vitesse dépend de la concentration en un seul réactant : v = k . (A)
et la constante de vitesse, k, s'exprimera en T-1
Réaction d'ordre 2 apparent
La vitesse, ici, varie avec en fonction d'une concentration au carré : v = k . (A)2 ou v = k . (A) . (B)
et la constante de vitesse, k, s'exprimera en M-1T-1
QUELQUES EXEMPLES DE RÉACTIONS CLASSIQUES
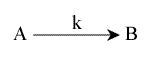
Cette réaction est d'ordre 1 apparent
Attention :
Le mot "apparent" doit être compris dans le sens de "qui apparait" ou "que l'on observe". Comme vous verrez plus bas dans ce chapitre, selon la méthode que l'on utilise pour mesurer la cinétique, ce qui apparait peut cacher des phénomènes plus complexes.
d(A) / dt = - d (B) / dt = -k (A)
En séparant les variables: d(A) / (A) = -k dt <=> Ln (A) = -k t + constante
Conditions initiales :
à t = 0, on a par exemple (A) = (A)0 et (B) = (B)0 = 0
Dans ce cas: (B) = (A)0 - (A) et constante = Ln (A)0
D'où : Ln (A) = -k t + Ln (A)0
et Ln ( (A) / (A)0 ) = -k t
(A) = (A)0 e-kt
avec (B) = (A)0 - (A)
donc (B) = (A)0 (1 - e-kt)
On peut facilement connaitre k même si on ne connait pas (A)0 en mesurant (A) puisque :
Ln (A) = -kt + Ln (A)0
En traçant Ln (A) = f(t), on obtient une droite dont le coefficient directeur est -k, qui ne dépend donc pas de (A)0. L'ordonnée à l'origine (ou intercept) de cette droite donne Ln (A)0.
Par contre, si on mesure (B), même pour un intervalle de temps très petit, on ne pourra connaître k qu'à (A)0 prés puisque :
(B) = (A)0 (1 - e-kt).
En utilisant le développement limité, autour de t = 0, de e-x = e0 - x = 1 - x :
(B) = (A)0 (1 - 1 + kt ) = (A)0 kt.
La pente de la droite obtenue en portant la variation initiale de B en fonction de t donne (A)0 k.
Mais, si on connait (A)0, on peut déterminer graphiquement k en traçant Ln [( (A)0 - (B) ) / (A)0 ] en fonction du temps.
En effet, connaissant (B) et (A)0 :
(B) = (A)0 - (A) <=> (A) = (A)0 - (B) Ln [ (A) / (A)0 ] = -kt
Ln [( (A)0 - (B) ) / (A)0 ] = Ln [ 1 - ( (B) / (A)0 ) ]= -k t
Remarque :
Ceci revient à tracer la variation de concentration de B par rapport à sa valeur finale, soit (A)0 - (B), normalisée par la variation maximale de la mesure (soit (A)0).
On retrouvera cette façon de procéder dans beaucoup d'exemples différents par la suite.
Complément :
Ce genre de cinétique d'ordre 1 s'observe dans plusieurs cas: par exemple la dénaturation thermique d'une protéine, ou sa dénaturation en présence d'un gros excès d'agent dénaturant.
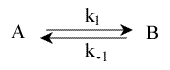
d(A)/dt = - d(B)/dt = - k1(A) + k-1(B)
Conditions initiales: par exemple (B)0 = 0 donc (B) = (A)0 - (A)
Remarque :
La variation de A, d(A) / dt , provient de A qui se transforme en B, avec un signe moins pour dire que A diminue (- k1(A) ) ainsi que de B qui se transforme en A, avec un signe plus puisque A augmente ( + k-1(B) ). En remplaçant (B) par [ (A)0 - (A) ], puis en séparant les variables :
d(A) / dt = - k1(A) + k-1 [ (A)0 - (A) ] = k-1(A)0 - ( k1 +k-1) (A)
d(A) / [ k-1(A)0 - ( k1 + k-1) (A) ] = dt
Pour simplifier l'écriture, on pose :
β = k1 + k-1
α =k-1(A)0 et (A) = x.
Remarque :
α et β sont des constantes
L'expression devient : dx / (α - βx ) = dt
qui donne, en intégrant : (- 1/ β ) Ln (α - βx ) = t + constante
à t = 0, (A) = (A)0 = x0
d'où : constante = (- 1/ β ) Ln (α - β x0 )
Et :
(- 1/ β ) Ln [ (α - β x) / (α - β x0 ) ] = t
Ln [ (α - β x) / (α - β x0 ) ] = - β t
Attention :
Il s'agit d'une réaction équilibrée et nous n'en avons pas encore tenu compte. Le formalisme mathématique doit rendre compte du mécanisme réactionnel dans sa globalité.
Si l'on étudie, en cinétique, cette réaction équilibrée, la notion d'équilibre doit être obligatoirement introduite dans l'expression décrivant cette étude cinétique. Lorsque l'équilibre est atteint, les concentrations mesurables en A et B sont constantes. On ne peut plus rien mesurer en cinétique lorsque l'on atteint les temps d'équilibre. Il faut impérativement introduire cette notion d'équilibre dans le formalisme de cette cinétique. Pour cela, on utilise les limites à l'infini.
Quand t → +00, Ln [ (α - β x) / (α - β x0 ) ] → -00 puisque β > 0 donc - β < 0
Ce qui n'est possible que si : α - β x00 = 0 soit x00 = α / β
Ln [ (α - β x) / (α - β x0 ) ] = Ln [ ((α / β ) - x)) / ((α / β ) - x0 ) ]
= Ln [ ( x00- x ) / ( x00 - x0 ) ] = - β t
En remplaçant α, β et x par leurs valeurs, on obtient :
(A)00 = k-1 (A)0 / ( k1 + k-1 )
et
Ln [ ((A)00 - (A) ) / ((A)00 - (A)0 ) ] = - ( k1 + k-1 ) t
Il est donc facile de déterminer la somme k1 + k-1 en traçant Ln [((A)00 - (A)) / ((A)00 - (A)0 )] en fonction du temps.
Remarquez que c'est encore la variation de la concentration mesurée par rapport à sa valeur finale, normalisée par la variation maximale, que l'on utilise.
Pour atteindre les valeurs individuelles des constantes cinétiques, il faut utiliser l'équilibre.
(A)00 = (A)eq : les concentrations sont constantes parce que, à l'équilibre, la vitesse macroscopique est nulle.
La vitesse microscopique de formation de A à partit de B est égale à la vitesse microscopique de destruction de A, c'est-à-dire :
k1 (A)eq= k-1 (B)eq <=> (B)eq / (A)eq = k1 / k-1
On pose: K = k1 / k-1 (dans laquelle K est appelée constante d'équilibre) ce qui donne
(A)00 = (A)0 / ( K + 1 )
On peut calculer (B)00 et (B) , de la même façon :
(B)00 = (A)0 - (A)00 = (A)0 - ( (A)0 / ( 1 + K ) ) = K (A)0 / ( 1 + K )
Si la concentration en B est plus facile à mesurer, il est aisé de voir que l'on obtient k1 + k-1 en traçant soit Ln [ ( (B)00 - (B) ) / ( (B)00 - (B)0 ) ] soit (dans le cas où la concentration initiale de B est nulle) Ln [ ( (B)00 - (B) ) / (B)00 ] , en fonction du temps.
Dans tous les cas, on connait donc la somme k1 + k-1 par l'étude cinétique, ce qui donne accès aux valeurs individuelles de k1 et de k-1 , puisque la position de l'équilibre donne K =k1 / k-1
Exemple :
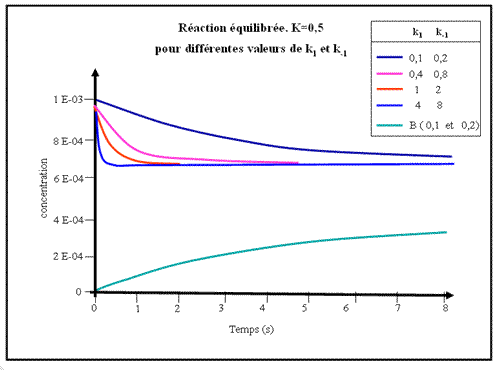
Figure.1a - La réaction est réversible avec K= 0,5.
Le même équilibre est atteint plus ou moins rapidement selon les valeurs de k1 et de k-1 (en gardant toujours le rapport k1 / k-1 constant).
Exemple :
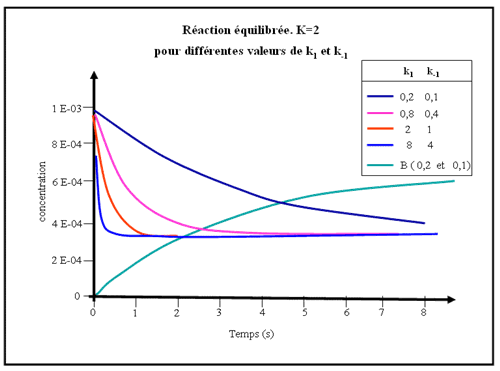
Figure.1b - La réaction est réversible avec K= 2.
Le même équilibre est atteint plus ou moins rapidement selon les valeurs de k1 et de k-1 (en gardant toujours k1 / k-1 constant).
Nous ne traiterons pas en détail ce cas général, car, bien souvent, l'un des réactifs est en excès (B par exemple) si bien que sa concentration ne change pratiquement pas au cours de la réaction:
(B) = (B)0.
Dans ce cas :
d(C)/dt = k1(A).(B)0 - k-1(C)
On peut écrire: kf = k1 (B)0
kf est la constante de pseudo premier ordre de formation de C à partir de A et B, B étant en excès. La terminologie "pseudo" utilisée ici, et que nous verrons souvent, est équivalente à "apparent". Dans ce cas précis, la vitesse de formation de C est d'ordre 2 réel mais comme B est en grand excés, sa concentration est constante et la cinétique est de pseudo ordre 1 : elle ne dépend en fait que de la concentration en A. Il est facile de vérifier que les dimensions de kf sont bien temps-1 . La constante de vitesse de formation de C est donc appelée constante de pseudo premier ordre alors que k1 est une constante de second ordre (en M-1 T-1 ).
En utilisant les conclusions du paragraphe précédent, la constante de vitesse d'établissement de l'équilibre est :
kexp = kf + k-1 = k1 . (B)0 + k-1
Bien entendu, dans le cas où aucun réactif n'est en excès, nous avons une constante de vitesse d'établissement de l'équilibre qui est : kexp = k1 .(A) (B) + k-1, dont l'expression analytique est beaucoup plus compliquée.
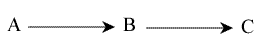
Il s'agit, ici, de réactions consécutives.
Equations utilisées :
1) d(A) / dt = - k1 (A)
La disparition de A ne dépend que de la concentration en A et de rien d'autre.
2) d(B) / dt = k1 (A) - k2 (B)
La variation de la concentration en B dépend de A qui se transforme en B, et de la transformation de B en C
3 ) d(C) / dt = k2 (B)
L'apparition de C ne dépend que de de la concentration en B
Résolution :
1→: (A) = (A)0e-k1t comme avant.
2→ : d(B) / dt = k1 (A)0 e-k1t - k2 (B).
On pose : (B) = u e-k2t avec u = f (t)
En remplaçant cette valeur de B dans l'équation différentielle, on trouve :
d(B)/dt = ( du / dt ) e-k2t - k2 u e-k2t = k1 (A)0 e-k1t - k2 u e-k2t
On en déduit que : du / dt = k1 (A)0 e(k2-k1)t soit u = [ k1 (A)0 / (k2 - k1 ) ] e(k2 - k1)t + Cste
D'où : (B) = [ k1 (A)0 / ( k2 - k1 ) ] e(k2 - k1)t + Cste ] e-k2t
La valeur de la constante ne peut être déterminée qu'en précisant les conditions initiales de la réaction.
Conditions initiales: à t = 0 (B)0 = 0
D'où : [ k1 (A)0 / (k2 - k1 ) ] + Cste = 0 <=> Cste = - k1 (A)0 / (k2 - k1 )
et : (B) = [ k1 (A)0 / (k2 - k1 ) ] e (k2 - k1 )t e-k2t - [ k1 (A)0 / (k2 - k1 ) ] e-k2t
soit : (B) = [ k1 (A)0 / (k2 - k1 ) ] [e-k1t - e-k2t]
3→ : Enfin, (C) = (A)o- (A) - (B) = (A)o { 1 - e-k1t - [ k1 / (k2 - k1 ) ] [ e-k1t - e-k2t
(C) = (A)o { k2 [ 1 -e-k1t] - k1 [ 1 - e-k2t ] } / (k2 - k1 ) ] }
* On remarque que, quand t →00, (C) → (A)0, comme il est normal
* (B) passe par un maximum lorsque d(B)/dt = k1 (A) - k2 (B) = 0.
En remplaçant (A) et (B) par leurs valeurs en fonction du temps, on voit que ceci est vrai pour un temps appelé tmax tel que : tmax = [ Ln ( k1 / k2 ) ] / (k2 - k1 ).
Exemple :
Les figures ci-dessous montrent les tracés des concentrations en A, B et C pour plusieurs jeux de valeurs des constantes de vitesse
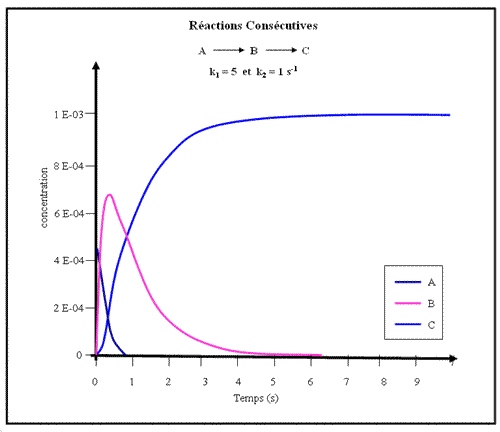
Figure.2- Deux réactions consécutives (avec les constantes de vitesse indiquées). L'intermédiaire B apparaît temporairement avec une concentration maximale élevée.
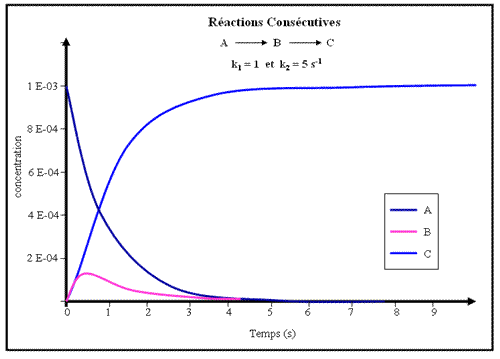
Figure.3- Deux réactions consécutives (avec les constantes de vitesse indiquées). L'intermédiaire B apparaît temporairement. Remarquer que la concentration maximale de l'intermédiaire est beaucoup plus faible que dans la figure.2.
NOTION D'ÉTAPE DÉTERMINANTE
Les deux graphes ci-dessous montrent les concentrations des composés B et C pour deux réactions consécutives A → B → C
Dans le premier cas, la première étape devient de plus en plus rapide par rapport à la seconde. Pour les valeurs de k1 = 2 et 5 s-1, on voit nettement un retard à l'apparition du dernier composé C. Pendant ce temps, le composé B s'accumule sensiblement pour les temps intermédiaires (de l'ordre de 0.2 à 3 s).
Mais quand k1devient grand devant k2, on voit que l'apparition de C devient quasiment superposable à ce qu'elle est (trait tireté) pour une simple réaction A → C, pourvu que la constante de vitesse de cette dernière soit k = 1 s-1. La vitesse d'apparition du dernier produit est donc limitée par la réaction la plus lente.
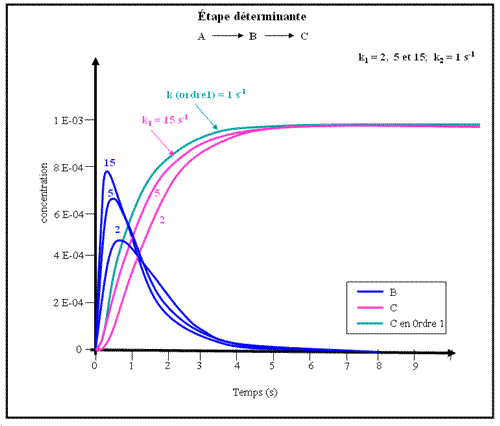
Figure.4- Etape déterminante (cas n°1)
Il en est de même dans le second exemple, où maintenant c'est la deuxième étape qui devient rapide par rapport à la première.
Ici encore, l'apparition de C est quasiment la même pour la réaction à deux étapes (pour k2=30 s-1) et pour la réaction A → C (avec k = 1 s-1).
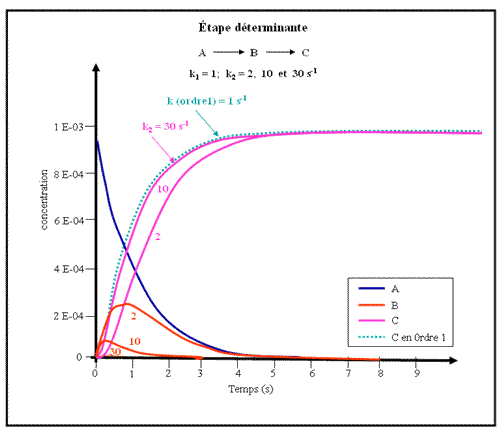
Figure.5- Etape déterminante (cas n°2)
On peut donc généraliser ce résultat en disant que, dans une chaîne de réaction (aussi longue soit elle pourvu qu'elle soit linéaire, c'est à dire sans boucle) la vitesse d'apparition du dernier produit de la chaîne est limitée par l'étape la plus lente. On voit toutefois, que cette conclusion n'est parfaitement vérifiée que s'il existe (au moins) une étape beaucoup plus lente que les autres (dont la constante de vitesse est 10-50 moins grande que les autres).
On vérifie par ailleurs, que le composé intermédiaire (B ici) apparaît en proportion non négligeable dans le milieu, au moins pendant une partie du déroulement de la réaction, à chaque fois que l'étape lente est la seconde. On peut également généraliser cette conclusion sous la forme suivante: les intermédiaires s'accumulent pendant une certaine fraction du temps d'une série de réactions consécutives, à condition qu'ils soient fabriqués dans une étape rapide et détruits dans une étape lente. Pratiquement, cela signifie que l'on peut espérer "voir" les intermédiaires qui précédent les étapes très lentes.
