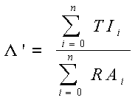Complément :
Vous trouverez, ici, les compléments des cours audio-vidéo de l'allostérie
Expérimentalement, on observe que :
Pour la fixation de ligand à l'équilibre les courbes de saturation des sites ne suivent pas toujours une loi hyperbolique, correspondant à la fixation sur une seule catégorie de sites. .
Pour les cinétiques enzymatiques, les courbes représentant la vitesse en fonction de la concentration en substrat, la forme n'est pas non plus hyperbolique
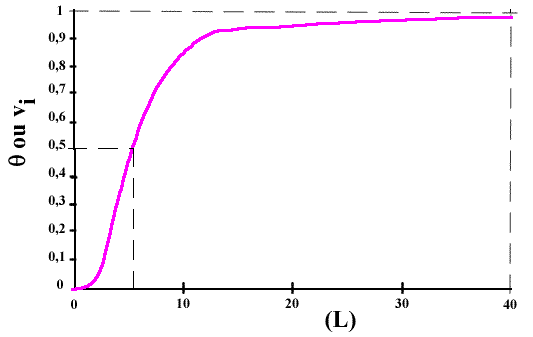
Comme dans l'exemple ci-dessus, la courbe de saturation est d'allure sigmoïde (en forme de S), ce qui signifie que l'affinité, initialement faible (démarrage lent de la fixation, en présence de concentration faible de ligand), augmente ensuite rapidement de telle façon que la fixation semble passer par un seuil, aux environs de la demi saturation. On appelle ce phénomène coopérativité. Remarquez que la quantité en ordonnée est θ (fixation à l'équilibre) ou la vitesse initiale vi (cinétique enzymatique).
Ce comportement particulier se retrouve dans de nombreuses enzymes clés de chaines métaboliques. Par exemple :
Aspartate transcarbamylase (ATCase) qui commande une étape précoce de la synthèse des nucléotides pyrymidiques.
Thréonine désaminase (TDase) impliquée dans la première étape de la fabrication de l'isoleucine à partir de la thréonine, l'oxydation de la thréonine en oxobutyrate en présence de pyridoxal phosphate :
HOOC-CHNH2-CHOH-CH3 → HOOC-CO-CH2-CH3
La glycogène phosphorylase (GPase) qui catalyse la dépolymérisation du glycogène selon :
(Glucose)n → (Glucose)n-1 + G1P
De plus l'activité de ces enzymes est régulée (inhibition ou activation) par la concentration des produits ou réactifs finaux de la chaine métabolique: l'ATCase est inhibée par l'ATP et activée par le CTP; la TDase inhibée par l'isoleucine et activée par la valine; la Gpase activée par l'AMP. Comme ces inhibiteurs ne se fixent pas sur les sites catalytiques et qu'ils ont une structure chimique très éloignées de celles des substrats, on les a qualifiés d'effecteurs allostériques. Ces deux phénomènes (coopérativité et allostérie) sont liés par un mécanisme moléculaire commun. Ce mécanisme se retrouve aussi bien dans la fixation à l'équilibre que dans la cinétique enzymatique.
Manifestation quantitative de la coopérativité
On suppose initialement l'existence de plusieurs sites de fixation du ligand (ou substrat) et une occupation soit nulle, soit totale de tous les sites d'un récepteur.
L'équilibre s'écrit alors :
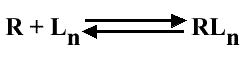
et la constante d'équilibre :
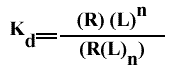
La saturation est représentée par :
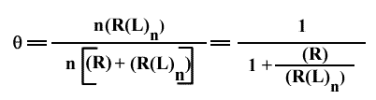
D'où :
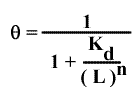 ET
ET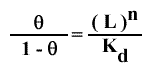
Cette expression donne :
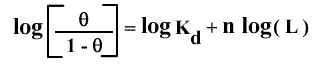
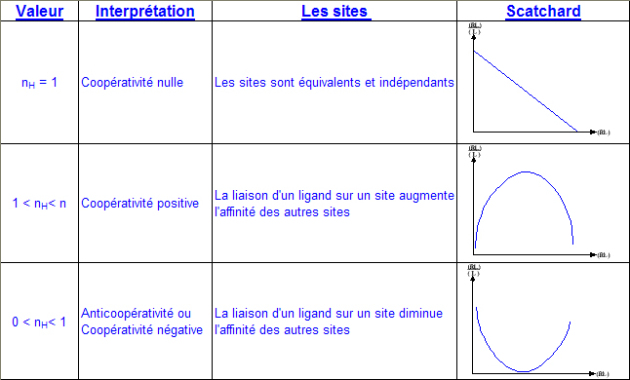
Le graphe correspondant, où on porte log (θ / (1-θ)) en fonction de log (L), s'appelle le graphe de Hill, du nom du physiologiste qui l'a proposé le premier. La pente de la droite obtenue est n (nombre de sites) et son ordonnée à l'origine - log (Kd) . Cette relation n'est valable que dans le cas limite (jamais observé en fait) où n'existent que la forme libre et complètement saturée du récepteur. Dans cette situation, toute molécule de récepteur qui a déjà fixé un ligand voit son affinité augmenter infiniment telle que les autres sites se saturent immédiatement. On parle alors d'une coopérativité maximale. A l'autre extrémité, si les sites sont équivalents et indépendants, la coopérativité est alors nulle.
On a vu que dans ce cas :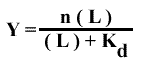 soit
soit 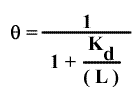
Donc :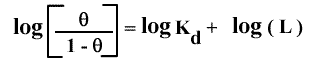
Ici, la pente du graphe de Hill sera égale à 1. On voit donc que la pente caractérise la coopérativité. De fait, les diagrammes de Hill sont rarements linéaires et on convient de prendre la pente de la courbe pour la demi- saturation ( θ= 1/2) que l'on appelle nH ou nombre de Hill.
Le nombre de Hill est compris entre 0 et n, n étant le nombre réel de sites de fixation. On peut distinguer 3 cas :
Lors d'une coopérativité positive, le nombre de Hill donne le nombre minimal de site.
Dans le cas où on observe une courbe sigmoïde en cinétique enzymatique, on suppose que la vitesse observée est proportionnelle à l'occupation des sites substrats: la saturation correspond à Vm et donc
θ = v / Vm .
Ceci donne donc que :
θ / (1-θ ) = v / (Vm - v)
et c'est le log de cette dernière valeur que l'on utilise alors dans les diagrammes de Hill.
Modélisation de la coopérativité selon Monod, Wyman et Changeux
Dans un article très fameux de 1965, J.Monod, J.Wyman et J-P Changeux (J.Mol.Biol, 12, 88) ont proposé un modèle général de la coopérativité. Ces auteurs sont partis des observations suivantes :
la nature oligomérique de la plupart (sinon tous) des "récepteurs" ou enzymes ayant un caractère coopératif,
la disparition réversible du caractère coopératif quand on dissocie les sous-unités,
l'existence d'effecteurs allostériques qui activent ou inhibent la réaction enzymatique en changeant aussi la valeur de nH.
En général, les activateurs diminuent la coopérativité tandis que les inhibiteurs l'augmentent.
Les auteurs proposent un modèle général basé sur les principes suivants :
On définit un protomère par la présence d'un seul site substrat (ou ligand) et d'un seul site effecteur. Un protomère peut être constitué de deux sous-unités, fixant respectivement les deux composés (substrat-ligand et effecteur).
Une protéine coopérative contient plusieurs protomères identiques, disposés selon un assemblage symétrique (au moins un axe de symétrie).
La protéine existe sous deux conformations différentes, toutes deux symétriques, appelées R (relaxée) et T (tendue). L'assemblage R ne contient que des protomères identiques de conformation r. L'assemblage T ne contient que des protomères identiques de conformation t.
Le passage de la conformation R à T est réversible.
Les protomères de conformation r et t ont des affinités différentes pour leurs ligands (substrat-ligand et effecteur).
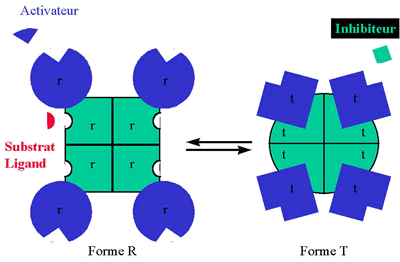
Sous une forme schématique, et pour un oligomère à quatre protomères, cela donne la figure ci-dessus dans le cas où :
Seules les sous unités r fixent le substrat-ligand (pour la sous-unité dite catalytique) et l'activateur (pour la sous-unité dite régulatrice).
Les sous unités catalytiques sous la forme t ne fixent pas du tout le substrat-ligand; les sous-unités régulatrices sous la forme t fixent l'inhibiteur.
Dans le cas plus général où le substrat ligand peut se fixer sur les sous-unités catalytiques, on définit les constantes d'affinités Kr et Kt correspondantes. Pour représenter ce système, il suffit de définir les constantes d'équilibres Kr et Kt pour la fixation du substrat-ligand et la constante d'équilibre L entre les formes R et T :
Kr= 4.(R).(L) / (RL) = 3.(RL).(L) / [ 2.(RL2) ] = 2.(RL2).(L) / [ 3.(RL3) ] = (RL3).(L) / [ 4.(RL4) ]
Kt= 4.(T).(L) / (TL) = 3.(TL).(L) / [ 2.(TL2) ] = 2.(TL2).(L) / [ 3.(TL3) ] = (TL3).(L) / [ 4.(TL4) ]
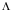 = (T) / (R)
= (T) / (R)
On en déduit que :
(RL) = 4 (R).(L) / Kr que l'on écrit = 4 (R) α en posant: (L) / Kr = α
(RL2) = 3.α (RL) / 2 = 6 (R) α2
(RL3) = 2.α (RL2) / 3 = 4 (R) α3
(RL4) = α (RL3) / 4 = (R) α4
(TL) = 4 (T).(L) / Kt que l'on écrit = 4 (T) . (L) / Kr Kr / Kt .
On pose : C=Kr / Kt et on rappelle que: (T) = ![]() (R)
(R)
donc : (TL) = 4
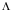 (R) C a
(R) C a et :
(TL2) = 3 C α (TL) / 2 = 6
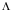 (R) C2 α2
(R) C2 α2
(TL3) = 2 C α (RL2) / 3 = 4
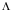 (R) C3 α3
(R) C3 α3
(TL4) = C α (TL3) / 4 =
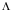 (R) C4 α4
(R) C4 α4
La définition de θ est telle que : 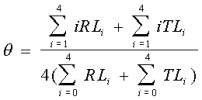
Ce qui donne, en remplaçant terme à terme par leurs valeurs : 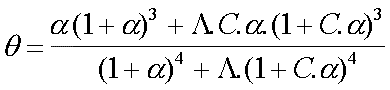
que l'on peut généraliser au cas d'un nombre quelconque de sites n: 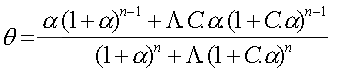
L'intérêt de ce modèle est multiple. En effet, il permet d'insister sur plusieurs faits importants :
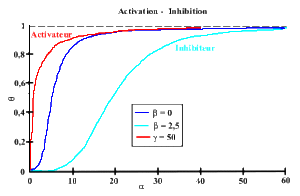
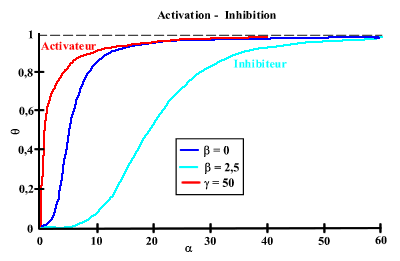
On peut simuler la plupart des comportements coopératifs observés. En effet, En jouant sur les valeurs de
 ou de C, on peut avoir des courbes de saturation (associées avec des valeurs du nombre de Hill) très différentes :
ou de C, on peut avoir des courbes de saturation (associées avec des valeurs du nombre de Hill) très différentes :
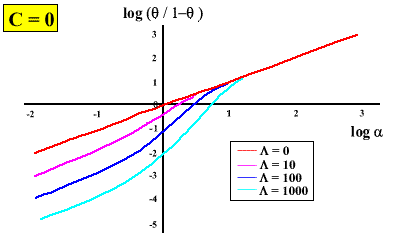
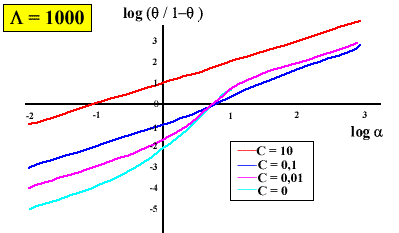
La coopérativité demande que le "récepteur" soit composé de sous-unités, existant dans deux conformations. Ces deux conformations t et r doivent avoir une affinité différente pour le substrat-ligand. En l'absence de substrat-ligand, l'équilibre entre les deux formes est déplacé vers la forme ayant la plus faible affinité pour ce substrat-ligand. Il est facile de voir que si c =1 (même affinité pour les 2 conformations),
 = 0 (seule la forme T existe) ou
= 0 (seule la forme T existe) ou 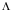 = 00 (seule R existe), le nombre de Hill devient égal à 1 (la coopérativité disparaît).
= 00 (seule R existe), le nombre de Hill devient égal à 1 (la coopérativité disparaît). La notion d'interaction entre les sites qui semblait correspondre à la coopérativité se ramène à l'existence de l'équilibre entre deux conformations et à la loi de Le Chatellier du déplacement de l'équilibre. En absence de ligand, la forme T de faible affinité est majoritaire. L'addition du ligand complexe le peu de forme R qui existe, ce qui a pour effet de déplacer l'équilibre entre T et R vers la forme R. La proportion de la forme R (de faute affinité) augmente donc, ce qui augmente l'affinité apparente du récepteur.
L'effet des effecteurs n'est que de déplacer l'équilibre entre T et R en complexant la forme T (inhibiteur) ou la forme R (activateur). Dans le cas où seuls T et R fixent respectivement l'inhibiteur I et l'activateur A avec les affinités KIT et KAR , on définit la constante d'équilibre entre toutes les formes T et R fixant les effecteurs par :
avec
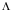 ' =
' =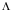 en absence d'effecteurs. On définit encore les grandeurs β = I / KIT et
en absence d'effecteurs. On définit encore les grandeurs β = I / KIT et 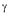 = A / KAR (analogues à la définition de α). De la même façon que ci-dessus on trouve que :
= A / KAR (analogues à la définition de α). De la même façon que ci-dessus on trouve que : 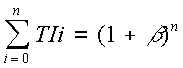 et
et 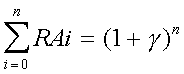
ce qui donne que :
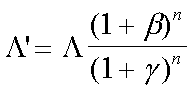
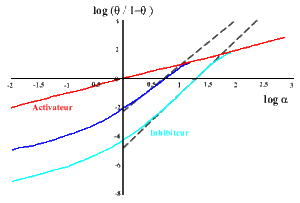
Il suffit de remplacer![]() par
par ![]() ' pour pouvoir calculer la forme des courbes (en saturation et selon Hill) obtenues pour des valeurs données de β et
' pour pouvoir calculer la forme des courbes (en saturation et selon Hill) obtenues pour des valeurs données de β et ![]() :
:
Saturation |
Hill |
Mais, une limite de ce modèle MWC est qu'il ne permet pas de rendre compte de l'anticoopérativité, puisque l'addition de ligand ne peut qu'augmenter l'affinité. L'adéquation de ce modèle avec les exemples les mieux connus de l'hémoglobine et de l'ATCase sera discuté ailleurs.