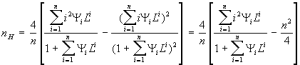Equation de Adair
La fixation d'un ligand sur un récepteur contenant des sites de fixation différents (quelque soit la raison de ces différences) a été étudiée par Adair et Wyman
On écrit tout d'abord les constantes microscopiques (dans le sens de la fixation):
K1 = (RL) / ( R )(L)
K2 = (RL2)/( RL )(L)
...
Kn = (RLn)/( RLn-1 )(L)
On écrit ensuite les équilibres suivants:
R + L
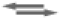(RL) avec 
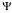1 = (RL) / ( R )(L) = K1R + 2 L
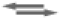(RL2 ) avec
2 = (RL2) / ( R )(L)2 = K1 K2R + 3 L
(RL3 ) avec
3 = (RL3) / ( R )(L)3 = K1 K2 K3..............................
R + n L
(RLn ) avec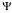
n = (RLn) / ( R )(L)n = K1 K2 ...Kn
et on pose
0 = 1
La saturation de ce récepteur est donné par:
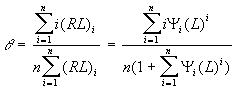 Adair - Equation 1 | Equation 1 |
On pose : 
si bien que: 
et que: 
Nombre de Hill
Le nombre de Hill est la pente de la représentation de log (θ /1-θ ) en fonction de log (L) (à demie saturation) c'est à dire la valeur de dlog ( θ /1-θ) / dlog (L) qui est égal à dLn ( θ /1-θ) / dLn(L).
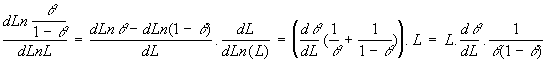
De plus, à demie-saturation 1 / [θ / (1-θ)] = 4
si bien que:
nH = 4.L.dθ / d (L) Equation 2
On peut introduire dans cette expression la valeur de d θ /d(L) qui est :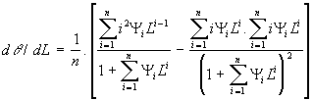 
si bien que:
 Nombre de Hill - Equation 3 | Equation 3 |
parce que, à demie saturation: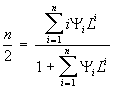
où L est ici la concentration du ligand à demie saturation, bien entendu.
