On peut schématiser ce qui se passe sur l'exemple de la fixations sur deux sites seulement. C'est le cas où la fixation sur un premier site diminue l'affinité de la fixation du ligand sur le second.
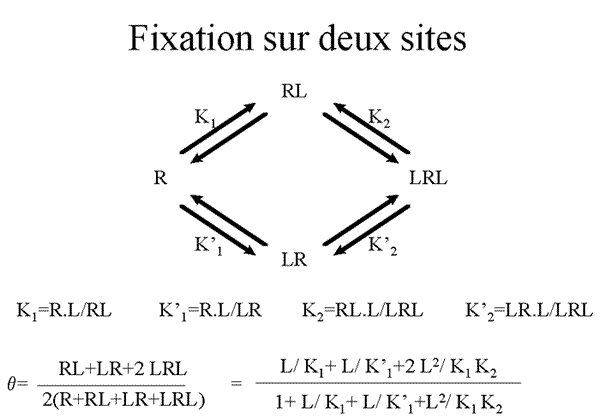
On a, évidemment, K1.K2= K’1.K’2
Les courbes ci-dessous sont obtenues dans les conditions suivantes : K1 = K’1 = 1 et K2 = K’2 = 20 dans l’unité que l’on veut, µM par exemple, ceci impose seulement que les concentrations en L soient dans la même unité). Le graphe direct montre que la fixation commence comme avec un seul site de haute affinité (K1 = 1), pour trainer ensuite, comme on pouvait s’y attendre:
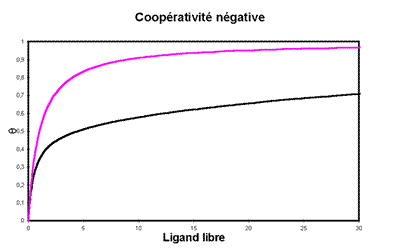
Il est facile de confondre la courbe noire avec une courbe de saturation ordinaire (en violet) dans laquelle le nombre de sites serait plus faible.
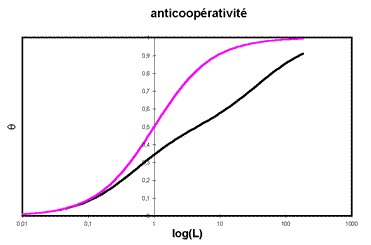
L'échelle logarithmique n'est pas beaucoup plus simple à cause des erreurs possibles sur les mesures. La seule chose claire est que la saturation n'est pas atteinte, comme on aurait pu le croire à partir de la figure précédente.
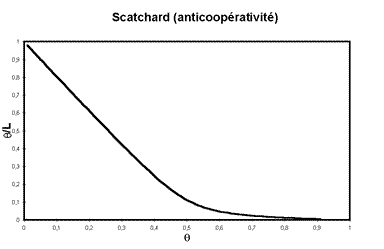
Le diagramme de Scatchard est très similaire au cas où coexistent des sites de haute et de basse affinité indépendants.
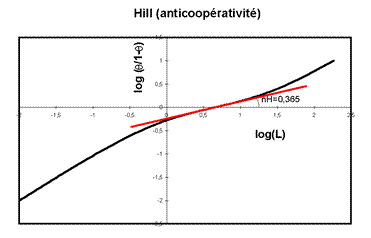
Le diagramme de Hill est beaucoup plus clair puisqu'on voit que nH= 0,365, ce qui prouve l'anticoopérativité
Remarque :
L'interprétation générale du schéma ci-dessus peut se faire en utilisant la valeur de nH tirée des équations de Adair (comme ci-dessous). On obtient bien entendu le même résultat quand K2 et K'2 K1.et K'1 .
Autres possibilités
Le cas décrit ci-dessus n'est pas le seul modèle permettant de mettre en évidence une anticoopérativité.
En effet, si on considère le schéma ci-dessus avec K1= K'2 et K2=.K'1 . Ceci correspond à l'existence d'un dimère de deux sous-unités différentes (fixant le ligand avec des affinités différentes) mais dont les sites sont indépendants l'un de l'autre (K1 =/= K2 et K'1=/= K'2, ce qui n'est pas contradictoire avec K1.K2 = K'1.K'2).
La valeur du nombre de Hill est donnée par (voir démonstration):
nH= 4 / (2 +
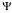1 / 
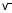
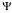2)
avec :
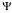1 = 1 / K1 + 1 / K’1 = 1 / K1 + 1 / K2 et
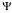2 = 1 / K1.K2 .
Il vient que :
1 /
2 = ( K1 + K2) / K1.K2
et donc : nH = 4 / ( 2 + ( K1 / K2 ) + K2 / K1).
Il est facile de montrer que nH
1.
En effet, que K1 soit inférieur ou supérieur à K2 on aura (K1 - K2)2
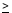0
et donc: K12 + K22
2 K1 K2 ou K12 + K22 + 2 K1K2
4 K1K2
ce qui donne que: (K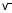1 + K2) /
K1K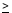2
2
ce qui fait que: 2 + ( K1 / K2 ) + ( K2 / K1 ) 4 et que: nH
1
En conclusion, un assemblage de deux sous-unités dissemblables fixant chacune le même ligand avec des affinités différentes se comporte comme un récepteur anticoopératif, même si la fixation des ligands ne provoque pas de changement de conformation de l'ensemble. On voit donc que l'anticoopérativité est un phénomène difficile à interpréter de façon non ambiguë. Heureusement, c'est une situation expérimentale rare.
