L’utilisation d’inhibiteurs compétitifs pour l’un des substrats permet de vérifier le mécanisme enzymatique entre les deux substrats.
Prenons un mécanisme ordonné et introduisons dans la cinétique un inhibiteur compétitif pour le second substrat ( B, dans ce schéma).
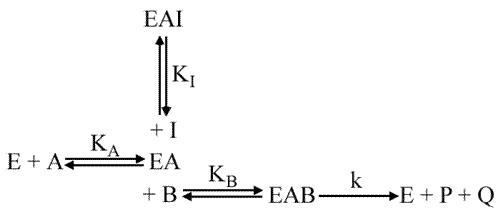
L'expérience est réalisée en deux temps: l'enzyme est d'abord incubée en présence d'une concentration variable en A, variable en I et saturante (et fixe) en B. Puis, dans une autre série, l'enzyme est incubée en présence d'une concentration variable en B, variable en I et saturante en A.
Equations utilisées :
(E)T = (E) + (EA) + (EI) + (EAB)
KA = (E) (A) / (EA)
KB = (EA) (B) / (EAB)
KI = (EA) (I) / (EAI)
v = k (EAB)
VM = k (E)T
Résolution :
[3] (EA) = [ KB / (B) ] (EAB)
[2] (E) = [ KA KB / (B) (A) ] (EAB)
[3] (EAI) = [ (I) / KI ] [ KB / (B) ] (EAB)
[1] (E)T = { 1 + [ KB / (B) ] [1 + ( (I) / KI )] + [ ( KB KA ) / ( (A) (B) ) ] } (EAB)
[6] v = ( k (E)T ) / { 1 + [ KB / (B) ] [1 + ( (I) / KI )] + [ ( KB KA ) / ( (A) (B) ) ] }
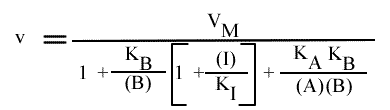
Et pour une représentation de Lineweaver-Burk :
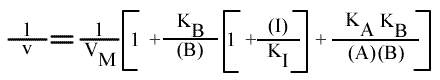
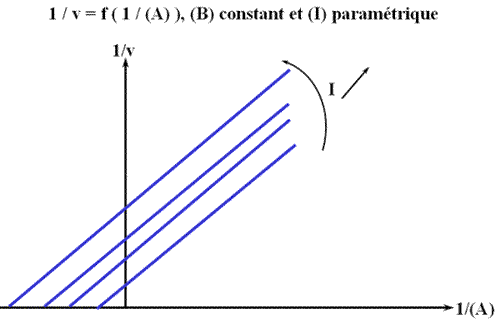
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (A) ), (B) fixe et (I) paramétrique :
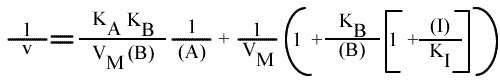
En traçant, pour une concentration en I donnée, une concentration en B fixe, 1 / v = f (1 / (A) ), on obtient une droite dont les caractéristiques sont :
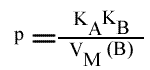
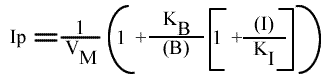
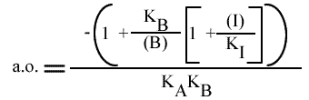
La pente est indépendante de la concentration en inhibiteur: toutes les droites seront donc parallèles (convergence à l'infini). Visuellement, en regardant le graphe 1 / v = f ( 1 / (A) ), (B) fixe et (I) paramétrique, l'interprétation est que I se comporte comme un inhibiteur in compétitif (ou conditionnel) vis à vis du substrat A.
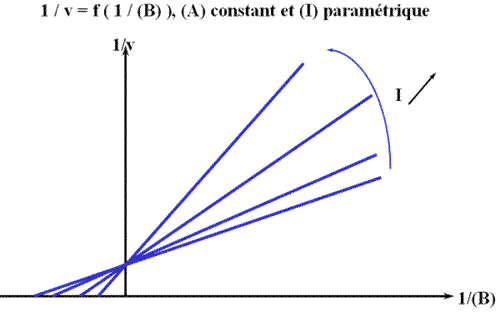
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (B) ), (A) fixe et (I) paramétrique :
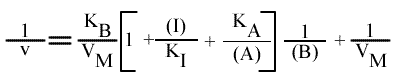
En traçant, pour une concentration en I donnée, une concentration en A fixe, 1 / v = f (1 / (B) ), on obtient une droite dont les caractéristiques sont :
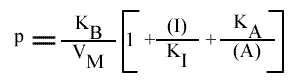
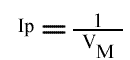
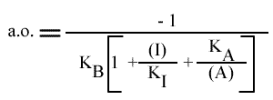
L'Ip est indépendant de la concentration en inhibiteur: toutes les droites convergeront sur l'axe des ordonnées. Visuellement, en regardant le graphe 1 / v = f ( 1 / (B) ), (A) fixe et (I) paramétrique, l'interprétation est que I se comporte comme un inhibiteur compétitif vis à vis du substrat B.
Voici les graphes:
Si, maintenant, on utilise un inhibiteur compétitif pour le premier substrat, A ici, les deux graphes 1 / v = f ( 1 / (A) ), (B) fixe et (I) paramétrique, et 1 / v = f ( 1 / (B) ), (A) fixe et (I) paramétrique, seront parfaitement symétrique; ils s'interprèteront tous les deux de la même façon: I est un inhibiteur compétitif pour le substrat A et un inhibiteur compétitif pour le substrat B.
Remarque :
L'interprétation des quatres graphes permet de vérifier le mécanisme ordonné (avec B qui se fixe en second) entre les deux substrats.
Complément :
La même démarche peut être faite pour les autres mécanismes et le tableau suivant résume les résultats ainsi obtenus:






