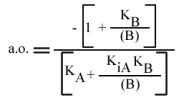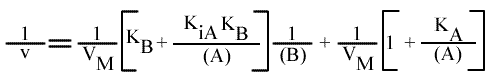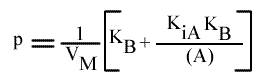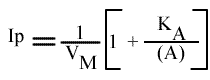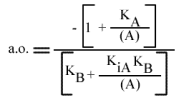Fondamental : Résolution en PER
Toute la résolution sera faite dans un premier temps dans l'hypothèse du pré-équilibre rapide, ( PER ), c'est-à-dire que les équilibres sont toujours vérifiés. En d'autres termes, les réactions de complexation des substrats avec l'enzyme ont atteint l'état d'équilibre avant libération du (des) produit(s).
Remarque :
On rappelle que la vitesse, v, exprimée dans toutes les équations qui suivent, est la vitesse initiale de la réaction.
Mécanismes impliquant la formation d'un complexe ternaire
Mécanisme aléatoire avec interaction entre les sites
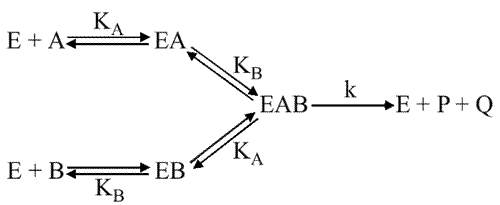
Le schéma est :
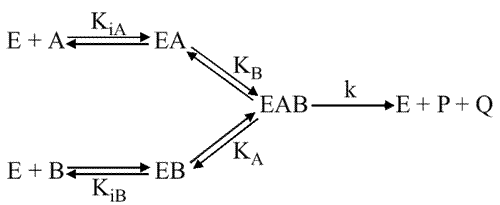
Avec : KiA différent de KA et KiB différent de KB.
Cela signifie que la fixation d'un substrat sur son site enzymatique modifie la fixation ultérieure de l'autre substrat sur son site.
Equations utilisées :
(E)T = (E) + (EA) + (EB) + (EAB)
KiA = (E) (A) / (EA)
KiB = (E) (B) / (EB)
KA = (EB) (A) / (EAB)
KB = (EA) (B) / (EAB) et KiAKB = KAKiB
v = k (EAB)
VM = k (E)T
Résolution :
[5] (EA) = [ KB / (B) ] (EAB)
[4] (EB) = [ KA / (A) ] (EAB)
[3] (E) = [ ( KB KIA ) / ( (A) (B) ) ] (EAB)
[1] (E)T = { 1 + [ KB / (B) ] + [ KA / (A) ] + [ ( KB KiA ) / ( (A) (B) ) ] } (EAB)
[6] v = ( k (E)T ) / { 1 + [ KB / (B) ] + [ KA / (A) ] + [ (KiA KB ) / ( (A) (B) ) ] }
[5] v = VM / { 1 + [ KB / (B) ] + [ KA / (A) ] + [ (KiA KB ) / ( (A) (B) ) ] }
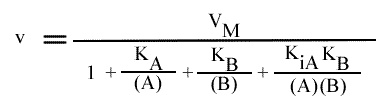
et pour une représentation de Lineweaver-Burk. :
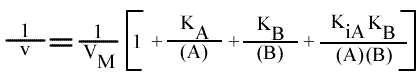
Méthode : Représentation de Lineweaver-Burk. : 1 / v = f ( 1 / (A) ), (B) paramétrique.
L'expression devient:
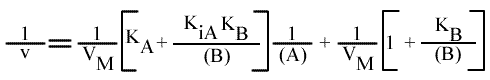
En traçant, pour une concentration en B donnée, 1 / v = f ( 1 / (A) ), on obtient une droite dont les caractéristiques sont :
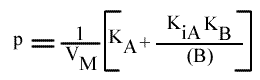
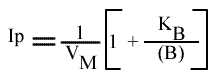
Les droites 1 / v = f (1 / (A) ) convergeront à gauche de l'axe des ordonnées, au point de coordonnées :
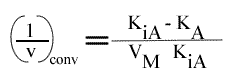 et
et 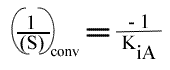
Pour décrire complètement le système, il faut calculer trois des constantes (KiA, KiB, KA, et KB) ainsi que la VM . Il faut donc tracer des graphes secondaires (au moins deux).
Graphes secondaires:
Si on trace les valeurs de Ip du graphe primaire [ 1 / v = f ( 1 / (A) ) ] en fonction de l'inverse de (B) :
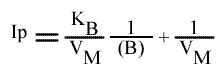
Cette équation est celle d'une droite :
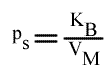
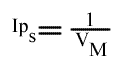
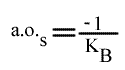
Si on utilise les pentes en fonction de (B):
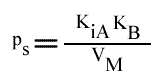
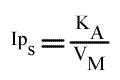
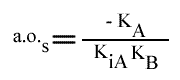
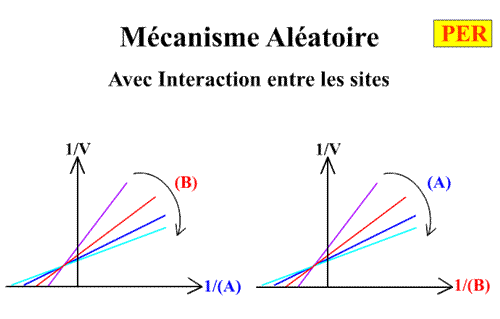
Méthode : Représentation de Lineweaver-Burk. : 1 / v = f ( 1 / (B) ), (A) paramétrique.
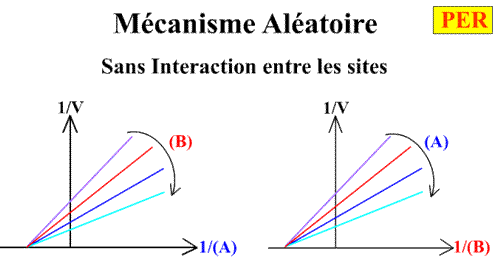
Voici les deux graphes primaires:
Premier cas limite : Mécanisme aléatoire sans interaction entre les sites
Dans ce cas KA = KiA et KB = KiB.
Cela signifie que la fixation d'un substrat sur son site enzymatique ne modifie pas la fixation ultérieure de l'autre substrat sur son site. Les sites sont indépendants.
En utilisant la même méthode de résolution, on trouve:
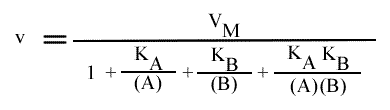
Pour une représentation de Lineweaver-Burk :

Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (A) ) : (B) paramétrique
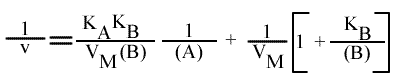
En traçant, pour une concentration en B donnée, 1 / v = f ( 1 / (A) ), on obtient une droite dont les caractéristiques sont directement obtenues à partir des expressions générales :
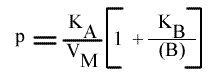
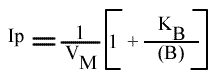
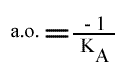
L'a.o. est indépendante de la concentration en substrat B: toutes les droites convergeront en ce point. Les coordonnées du point de convergence sont donc:
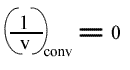 et
et 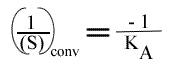
Graphes secondaires:
En traçant: p = f ( 1 / (B)):
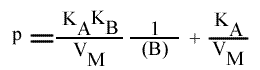
Cette équation est celle d'une droite :
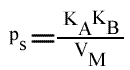
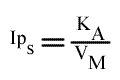
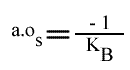
On peut tracer un autre graphe secondaire: Ip = f ( 1 / (B) ), mais on ne peut pas, bien évidemment, utiliser l'a.o.
Méthode : Représentation de Lineweaver-Burk. : 1 / v = f ( 1 / (B) ), (A) paramétrique.

Le résultat est symétrique du précédent.
Voici les deux graphes primaires:
Deuxième cas limite : Mécanisme ordonné
KiB = 0 et KA= 0. Pour simplifier l'écriture KiA devient KA

Cela signifie que B ne peut se fixer sur son site enzymatique que si A se trouve déjà fixé.
En utilisant la même méthode de résolution, on trouve:
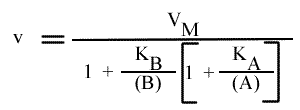
Pour une représentation de Lineweaver-Burk :
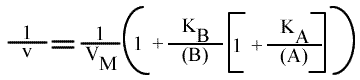
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (A) ), (B) paramétrique :
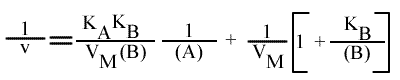
En traçant, pour une concentration en B donnée, 1 / v = f ( 1 / (A) ), on obtient une droite dont les caractéristiques sont :
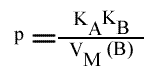
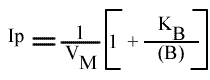
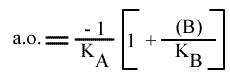
Les trois paramètres dépendent de la concentration en substrat paramétrique: le point de convergences des droites se trouve hors des axes.
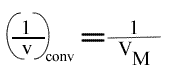 et
et 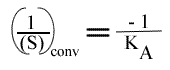
Graphes secondaires:
On peut utiliser les trois paramètres pour tracer un graphe secondaire. Ici, l'exemple traitera de l'utilisation de l'a.o.qui est un peu particulière dans ce modèle.
En traçant: a.o. = f ( (B) ):
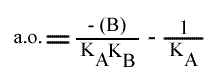
on obtient une droite :
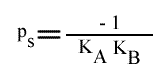
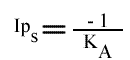
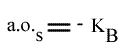
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (B) ), (A) paramétrique :
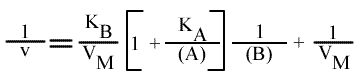
En traçant, pour une concentration en A donnée, 1 / v = f (1 / (B) ), on obtient une droite dont les caractéristiques sont :
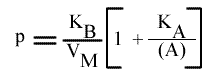
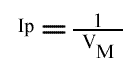
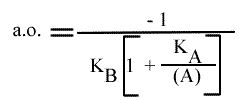
L'Ip est indépendant de la concentration en substrat B: toutes les droites convergeront en ce point. L'Ip ne pourra pas être utilisé pour construire un graphe secondaire. Les coordonnées du point de convergence sont donc:
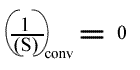 et
et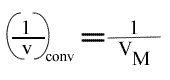
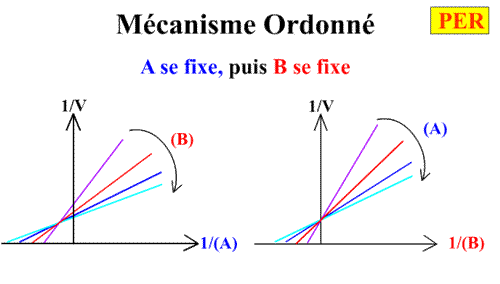
Voici les deux graphes primaires:
Mécanismes excluant la formation d'un complexe ternaire
Mécanisme Ping Pong
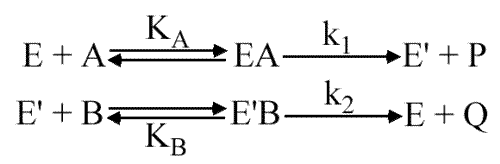
E' est l'enzyme modifiée (par acétylation, phosphorylation....). Le système ne peut être résolu que si la vitesse d'apparition de P est égale à celle de Q.
Equations utilisées :
(E)T= (E) + (EA) + (E'B) + (E')
KA = (E) (A) / (EA)
KB = (E') (B) / (E'B)
v = d(P) / dt = d(Q) / dt = k1(EA) = k2 (E'B)
VM = k1 (EA)Max = k2 (E'B)Max
Remarque :
La vitesse maximale est atteinte lorsque toute l'enzyme est complexée, soit : (E)T = (EA)Max + (E'B)Max
Résolution
[4] (E’B) = k1 (EA) / k2 et (E’B)Max = k1 (EA)Max / k2.
(E)T = (EA)Max (1 + ( k1 / k2 ) ) = (EA)Max ( k1 + k2 ) / k2
[5] VM = k1 (EA)Max = k1 k2 (E)T / ( k1 + k2 )
[2] (E ) = KA (EA) / (A)
[3] (E’) = KB (E’B) / (B)
[1] (E)T = (EA) [ 1 + KA / (A) ] + (E’B) [ 1 + KB / (B) ]
(E)T = (EA) {[ 1 + KA / (A) ] + [ 1 + KB / (B) ] k1 / k2}
[4] vi = k1 (E)T /{[ 1 + KA / (A) ] + [ 1 + KB / (B) ] k1 /k2}
= [ k1 k2 (E)T / (k1 + k2 )] / {k1 k2 / (k1 + k2 )} {[ 1 + KA / (A) ] + [ 1 + KB / (B) ] k1 / k2}
= VM / {[k2 / (k1 + k2 )] [ 1 + KA / (A) ] + [k2 / (k1 + k2 )] [ 1 + KB / (B) ] k1 / k2}
= VM / { 1 + [k2 / (k1 + k2 )] [ KA / (A) ] + [k1 / (k1 + k2 )] [ KB / (B) ] }
En posant:
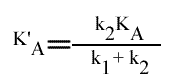 et
et 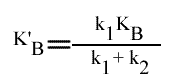
avec: 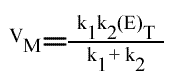
D'où: | 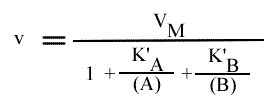 Mécanisme Ping pong :expression de la vitesse |
Et pour une représentation de Lineweaver-Burk :

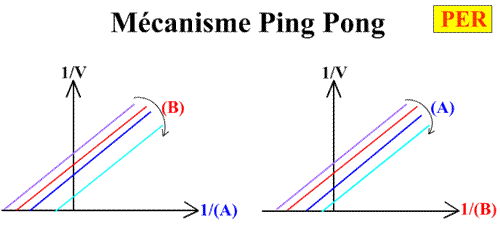
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (A) ), (B) paramétrique :
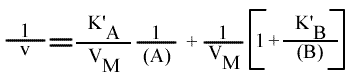
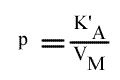
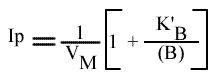
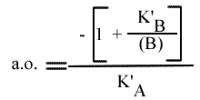
La pente est indépendant de la concentration en substrat B: toutes les droites seront donc parallèles: la convergence est à l'infini. La pente ne pourra pas être utilisée pour construire un graphe secondaire.
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (B) ), (A) paramétrique :
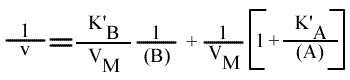
Cette expression est parfaitement symétrique de la précédente.
Voici les deux graphes primaires:
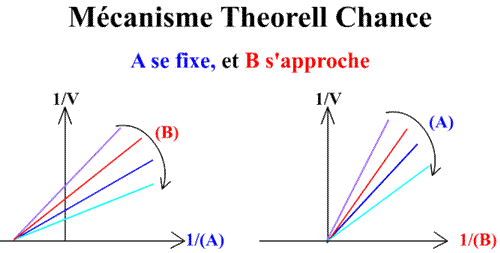
Theorell Chance
Le schéma est :
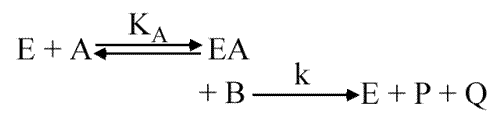
Ici, il n'y a pas de saturation possible en B.
Equations utilisées :
(E)T= (E) + (EA)
KA = (E) (A) / (EA)
v = d(P) / dt = d(Q) / dt = k (EA) (B)
VM = k (E)T
Résolution:
On trouve:
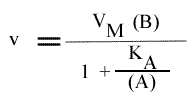
Et pour une représentation de Lineweaver-Burk :
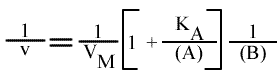
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (A) ), (B) paramétrique :
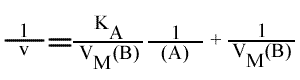
En traçant, pour une concentration en B donnée, 1 / v = f (1 / (A) ), on obtient une droite dont les caractéristiques sont :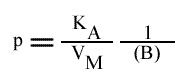
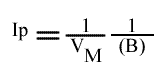
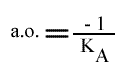
L'a.o. est indépendante de la concentration en substrat B: toutes les droites convergeront en ce point. L'a.o ne pourra pas être utilisé pour construire un graphe secondaire. Les coordonnées du point de convergence sont donc:
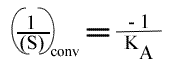
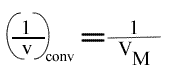
Méthode : Représentation de Lineweaver-Burk : 1 / v = f ( 1 / (B) ), (A) paramétrique :
En traçant, pour une concentration en A donnée, 1 / v = f (1 / (B) ), on obtient une droite dont les caractéristiques sont :
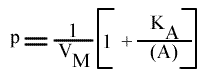
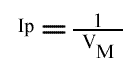

Un résultat directement fourni par les caractéristiques de ce graphe primaire, est que l'origine est indépendante de (A). Les droites 1 / v = f (1 / (B) )convergeront donc sur l'origine des axes, donc au point de coordonnées :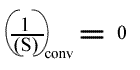
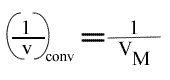
Voici les deux graphes primaires: