Le but des expériences de liaison à l'équilibre est de mesurer l'affinité de la fixation d'un "ligand" (substrat, inhibiteur, hormone, neurotransmetteur, anticorps, ...) sur un "récepteur" (enzyme, récepteur hormonal ou autre, antigène, ...). Il faut, bien évidemment, disposer d'une méthode qui permette de quantifier cette liaison, c'est-à-dire qui discrimine le complexe ligand-récepteur des réactants isolés, non complexés. On ne parle pas ici des méthodes permettant l'identification des partenaires d'un récepteur sans donner de renseignement sur l'affinité (co-immunoprécipitation, "overlay" après électrophorèse, double hybride ... ). Lorsque l'on souhaite étudier la liaison d'un ligand à un récepteur, cela implique, de fait, que la liaison soit spécifique donc saturable. En effet, d'une part le nombre de récepteur présent dans l'échantillon est fixe, donc le nombre de complexe ligand-récepteur pouvant être formé est limité, et d'autre part le récepteur ne permet pas à n'importe quelle structure de se lier dans son site. L'existence d'un récepteur est donc vérifiable par la saturation de la liaison.
La liaison d'un ligand sur son récepteur est spécifique, saturable et de haute affinité.
La mesure de la fixation
On peut généralement séparer physiquement les complexes récepteur-ligand des ligands libres qui sont souvent plus petits (surtout quand les récepteurs sont associés à des cellules). On utilise donc toutes les méthodes de séparation : selon la taille (filtration, dialyse, centrifugation...); selon la charge (électrophorèse, chromatographie d'échange d'ion ...) ou selon l'affinité vis à vis d'autres molécules (hydrophobicité, anticorps, précipitation des protéines par l'acide trichloracétique ...). Le ligand est généralement sous une forme qui permet d'en détecter une très faible concentration (radioactif, ou éventuellement fluorescent). Le résultat des mesures est donc de déterminer les concentrations des formes libre ( L ) et associée ( LF ) du ligand.
On peut aussi mettre en évidence l'association du ligand sur son récepteur par des méthodes de résonance plasmonique de surface (SPR) , de diffusion de translation dans des petits volumes, ou de calorimétrie.
Enfin, on peut utiliser le fait que la fixation d'un ligand change souvent les propriétés optiques (absorbance ou fluorescence) du récepteur. Le cas le plus simple et le plus connu est celui de l'hémoglobine.
On s'intéresse à la fixation à l'équilibre, ce qui suppose que ce dernier soit réalisé. Il est donc important de vérifier ce point (la quantité de ligand lié ne doit plus changer après un certain délai, à déterminer). C'est l'expérience préliminaire à toute étude de liaison. Pour cela, le récepteur est incubé en présence d'une forte concentration en ligand puis on mesure en fonction du temps la quantité de complexe. L'équilibre est atteint lorsque la concentration en complexe ligand-récepteur reste constante en fonction du temps.
Les liaisons en cause
Lorsque l'étude de la liaison entre le ligand et son récepteur fait appel à des techniques de séparation physique, on utilise souvent un ligand radioactif qui permet de mesurer la liaison sur de très faibles quantités de récepteur. Une expérience de liaison est réalisée classiquement de la façon suivante :
Dans un premier temps, le ligand radio marqué est incubé à concentration variable, en présence du récepteur pendant le temps nécessaire pour que l'équilibre soit établit. Le ligand libre (au sens de non lié) est séparé physiquement du ligand fixé et chaque concentration quantifiée par comptage radioactif. Nous disposons, ainsi d'un tableau de trois types de concentrations :
(L)T : la concentration totale du ligand mis en réaction
(L)l : la concentration du ligand libre, non lié
(L)F : la concentration du ligand fixé ( lié ). ( L)F correspond à la concentration en complexe ligand-récepteur.
Lorsque le récepteur est la seule structure à pouvoir lier le ligand, alors la concentration ( L)F correspond à la concentration en complexe ligand-récepteur. Le résultat attendu pour cette expérience est représenté par la courbe violette dans le graphe ci-dessous.
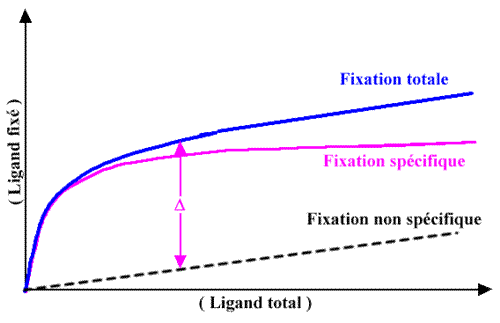
Mais, dans la majorité des cas en fait, la courbe de fixation se prolonge par une croissance continue qui ne correspond donc pas à une saturation d'un nombre limité de sites. Cela correspond à une fixation de très faible affinité (non spécifique) sur un grand nombre de sites. C'est la liaison non spécifique. On peut évaluer cette fixation non spécifique en traçant une droite parallèle à la fin de la courbe expérimentale passant par l'origine. La fixation spécifique est alors évaluée par différence ( 
) entre la fixation totale et la fixation non spécifique. La courbe violette correspond au tracé de en fonction de la concentration en ligand total. Seule cette courbe ( violette ) de liaison spécifique est exploitée dans un diagramme de Scatchard (voir plus loin) pour déterminer l'affinité du ligand pour son récepteur.
Donc, lorsque l'on détecte une liaison non spécifique, le protocole expérimental décrit ci-dessus donne en fait :
(L)T : la concentration totale du ligand radioactif mis en réaction
(L)1 : la concentration du ligand radioactif libre, non lié
(L)FT : la concentration du ligand radioactif fixé (lié) qui est, ici, la somme de deux sortes de fixation :
le ligand fixé de façon spécifique (L)Fsp
le ligand fixé de façon non spécifique (L)Fnsp
Pour arriver à quantifier correctement la liaison non spécifique, on incube le ligand radiomarqué, toujours à concentration variable avec le récepteur, mais, maintenant, en présence également d'un grand excès de ligand froid, non radio marqué. Une fois l'équilibre établit, le ligand libre est séparé physiquement du ligand fixé et chaque concentration quantifiée. Il ne faut pas oublier que seule la radioactivité est mesurée : ce qui n'est pas radioactif n'est pas quantifiable. Nous disposons toujours d'un tableau des trois sortes de concentrations :
(L)T : la concentration totale du ligand radioactif mis en réaction
(L)1 : la concentration du ligand radioactif libre, non lié, que l'on note souvent (L) simplement
(L)FT : la concentration du ligand radioactif fixé (lié) qui est, dans cette expérience, uniquement la liaison non spécifique(L)Fnsp. En effet, le ligand froid étant en grand excès par rapport au ligand radioactif, le récepteur sera occupé par le ligand froid.
Ainsi, la différence de ces deux expériences permet de mesurer la liaison spécifique.
Les grandeurs en cause
On dispose donc d'une courbe de liaison spécifique et saturable qu'il faut maintenant interpréter. On cherche l'affinité du ligand pour son site (mesurée par sa constante d'association, Ka ,qui est l'inverse de la constante de dissociation, Kd ) ainsi que le nombre de sites (qui peut être soit le nombre de sites dans l'échantillon considéré, soit le nombre de sites par récepteur).
On définit le taux de saturation du récepteur, Y :
Y = (L)F / (R)T
et le taux de saturation des sites, θ :
θ= (L)F / n (R)T
d'où : θ = Y / n
avec :
(R)T : concentration totale en récepteur, en protéine réceptrice
n : nombre de site de liaison par récepteur
Y représente le nombre de ligand lié par récepteur, en moyenne.
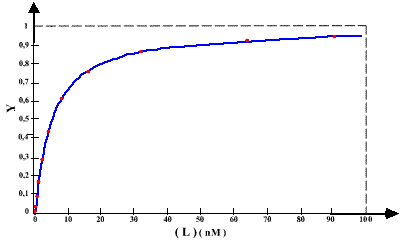
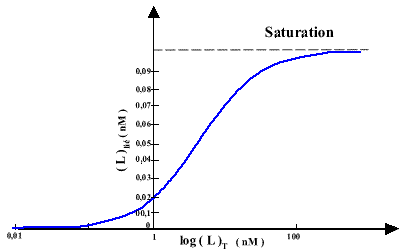
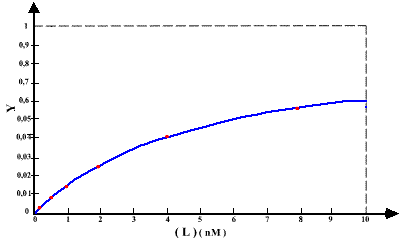
Expérimentalement , il faut pouvoir vérifier la saturation de la liaison spécifique. Pour cela il faut utiliser une large gamme de concentration en ligand et bien observer la courbe. Le graphe 1 montre une saturation évidente, ce qui est confirmé par le graphe 2 qui est une représentation en échelle semi-logarithmique des mêmes valeurs.
Graphe 1 :
Graphe 2 :
Attention :
L''allure sigmoïde de la courbe du graphe 2 s'explique, de fait, parce que l'échelle des abscisses est logarithmique. Cette représentation est très utile pour vérifier la saturation mais ne doit pas être sur interprétée, en posant par exemple, un phénomène de liaisons coopératives (voir plus loin).
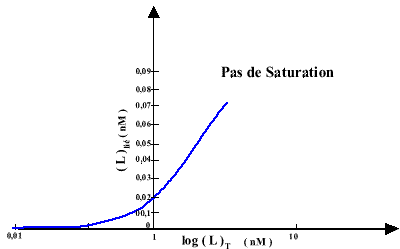
En observant le graphe 3, une interprétation hâtive conduirait à la même interprétation mais en reportant les valeurs obtenues sur un graphe en échelle semi-logarithmique (graphe 4), on voit immédiatement que le saturation n'est pas atteinte.
Graphe 3 :
Graphe 4 :
Fixation sur un seul site
Le modèle est :
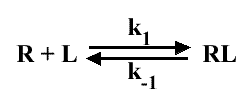
n = 1 donc Y = θ
Kd = (R) (L) /(RL) = 1 / Ka .
(L)T = (RL) + (L)
( R )T = (RL) + (R)
Y = (RL) / (R)T = (RL) / [ (RL) + (R) ]
Y = 1 / [1 + ( (R) / (RL) ) ] = 1 / [ 1+ (Kd / (L) ) ]
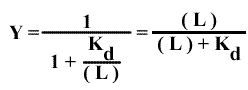
On peut traiter ces résultats en double inverse (représentation dite de Benesi-Hildebrand, analogue à un Lineweaver-Burk). L'habitude (qui est une seconde nature; c'est dire que la justification d'utiliser l'une ou l'autre des représentations n'est pas très forte) est d'utiliser un diagramme dit de Scatchard (en fait analogue à celui d'Eadie-Hofstee, utilisé en enzymologie).
Y= (L) / [(L) + Kd ]
1 – Y = Kd / [(L) + Kd ]
Y / [1 - Y] = (L) / Kd
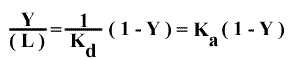
Le diagramme de Scatchard correspondant, Y / ( L ) = f ( Y ), donne donc une droite de pente -1/ Kd = - Ka et d'abscisse à l'origine 1 puisque n = 1 (un seul site).
Graphe 5 : Graphe de Scatchard
Si on ne connait pas (R)T :
Dans ce cas, on ne peut pas calculer Y et donc tracer le graphe de Scatchard. On reprend l'expression :
Y / (L) = (RL) / [ (R)T (L)] = Ka [ 1 - ( (RL) / (R)T )]
(RL) / (L) = Ka (R)T - Ka (RL)
En traçant (RL) / (L) = f ( (RL) ), on doit obtenir une droite dont les caractéristiques sont :
p = - Ka = - 1 / Kd
Ip= Ka (R)T
a.o.= (R)T
Graphe 6 :
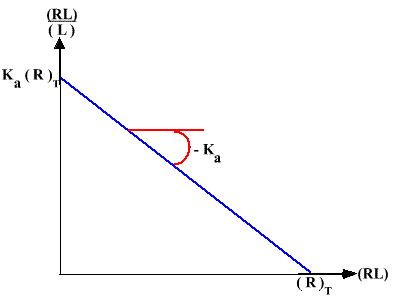
Ici, on peut mesurer (L) et (L)F = (RL) puis tracer le graphe (RL) / (L) = f ( (RL). On peut ainsi déterminer (R)T et Kd.
Lorsqu'on ne connait pas du tout la structure du récepteur (ni sa masse moléculaire, ni le nombre de site de liaison par protéine....), le graphe de Scatchard présenté ici s'interprètera ainsi : il y a une seule classe de sites indépendants et équivalents. Cela veut dire que même si la protéine réceptrice possède plusieurs sites de liaisons, ils ont tous la même affinité pour le ligand et il n'y a pas d'interaction entre eux, c'est-à-dire que la liaison d'un ligand sur un site ne modifie pas l'affinité d'un autre site. On raisonne alors en termes de site récepteur et non plus de protéine réceptrice. Ce modèle est tout à fait similaire à celui d'un seul site de fixation par récepteur en ce qui concerne la résolution. Et par abus de language, on parle de récepteurs.
Puisqu'on ne connait même pas la masse moléculaire du récepteur, c'est donc qu'il n'a pas été purifié. Les expériences de liaison à l'équilibre ont été réalisées avec un milieu complexe. La concentration du récepteur d'intérêt est proportionnelle à la concentration du matériel dans l'échantillon, (P)T (nombre de cellules, poids d'organe, protéines... par unité de volume).
(R)T = α . (P)T
avec :
(R)T : en mole / litre
(P)T : en g de protéines (ou nombre de cellules) / litre
α : en mole de ( site ) récepteur / g de protéine (ou nombre de cellules)
Le graphe de Scatchard permet d'atteindre la concentration totale en sites récepteurs mais ne permet pas de connaitre le nombre de sites par protéines réceptrices.
Inhibition de fixation
Bien entendu, tout agoniste ou antagoniste qui se fixe sur le même site que le ligand d' intérêt (l'hormone, le neurotransmetteur, le facteur de croissance...) se comporte comme un inhibiteur compétitif de cette liaison. On peut étudier la liaison de cet inhibiteur si on dispose d'une forme radioactive, comme on vient de le faire avec le ligand "endogène". Mais si on ne dispose pas de l' inhibiteur radioactif, on peut suivre le déplacement du ligand radioactif avec lequel il est en compétititon pour le même site.
On se trouve alors en présence de 2 fixations caractérisées par les équations suivantes :
Kd = (R). (L) / (RL) pour la fixation de L ( ligand radioactif )
KI= (R) . (I) / (RI) pour la fixation de I ( non radioactif ).
On mesure la radioactivité associée au récepteur, c'est à dire (RL). Si ni le ligand ni l'inhibiteur ne sont en excès par rapport au récepteur, le système conduit à deux équations quadratiques avec pour inconnues (RL) et (RI), un peu difficile à résoudre.
Si, par contre, le ligand et l'inhibiteur sont simultanément en excès par rapport au récepteur, on écrit seulement :
(L)T >> (R)T et (I)T >>(R)T
(L)T = (RL) + (L) avec : (L)T ~ (L) >> (RL)
(I)T = (RI) + (I) avec : (I)T ~ (I) >> (RI)
Kd = (R) (L) / (RL) d'où (R) = (RL) [ Kd / (L) ]
KI = (R) (I) / (RI) d'où (RI) = (R) [ (I) / KI ] = (RL) [ Kd / (L) ] [ (I) / KI ]
(R)T = (RL) + (R) + (RI) d'où (R)T = (RL) { 1 + [ Kd / (L) ] [ 1 + [ (I) / KI ] ] }
Y = (RL) / (R)T = 1 / { 1 + [ Kd / (L) ] [ 1 + [ (I) / KI ] ] }
Y = (RL) / (R)T = (L)T / { (L)T + [ Kd [ 1 + [ (I)T / KI ] ] }
Remarque :
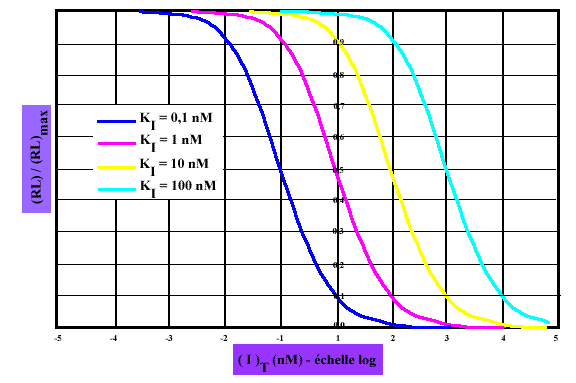
On peut noter en passant la concordance entre cette expression et celle obtenue pour l'inhibition compétitive des cinétiques michaëliennes (ce qui est la moindre des choses, vue la similitude des conditions). La mesure de Ki se fait alors en mélangeant le récepteur avec une concentration fixe de ligand chaud, auquel on ajoute ensuite des concentrations croissantes de l'inhibiteur. Le diagramme donné ci-dessous correspond au calcul avec (R)T= 0,1 pM et (L)T = Kd = 0,1 nM. On exprime les résultats de la fixation normalisés par la fixation maximale (en absence d'inhibiteur). On utilise une représentation semi logarithmique, plus favorable pour étudier les résultats sur une gamme étendue de concentrations. Il est facile de voir que les valeurs de ( I )T pour lesquelles on obtient un déplacement de 50% de la fixation maximale du ligand chaud correspond au KI. On a donc ici une méthode simple pour déterminer KI pour un inhibiteur dont on ne possède pas d'analogue radioactif.
Graphe 7
