Le pH peut agir sur plusieurs facteurs :
l'ionisation du substrat et / ou du produit
la structure des protéines : donc la stabilité de l'enzyme
la liaison du substrat à l'enzyme
l'activité catalytique de l'enzyme
Ceci explique que, expérimentalement, les réactions doivent se faire en milieu tamponné, donc avec un pH constant pendant toute l'expérience.
Le pH peut aussi jouer sur l'ionisation du substrat et/ou du produit. Dans ce cas, une étude préalable s'impose si l'état d'ionisation modifie les caractéristiques spectrales du composé que l'on dose lors de la cinétique. En d'autres termes, lorsque l'on utilise un composé chromophore, il faut, au préalable à toute mesure cinétique, savoir s'il y a ou non modification du coefficient d'absorption moléculaire ( ε ) du composé avec le pH.
Quant à la stabilité de l'enzyme en fonction du pH, elle est évaluée dans une expérience contrôle qui consiste à préincuber l'enzyme seule dans des solutions tampons de pH différents, puis elle est incubée dans la solution tampon d'étude en présence cette fois du substrat : cette expérience contrôle permet de voir les inactivations irréversibles de l'enzyme.
Dépendance du pH pour des enzymes michaeliennes
Les mesures de nombreuses activités enzymatiques en fonction du pH donnent des courbes qui passent par un maximum, montrant ainsi l'existence d'un pH optimum. On peut schématiser tous ces résultats sous une forme régulière idéalisée de courbe en cloche comme dans la figure ci-dessous.
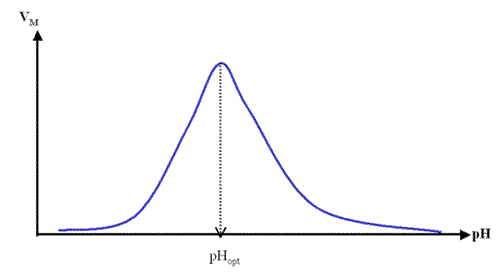
Cette forme de courbe est reliée à l'état d'ionisation de certains résidus d'acides aminés qui se trouvent dans un état d'ionisation précis indispensable à l'activité enzymatique. Au sommet de la courbe en cloche, l'enzyme a une activité maximale : elle est à son pH optimum de catalyse. La théorie simplifiée qui permet d'expliquer l'existence d'une activité enzymatique qui passe par un maximum en fonction du pH de la solution est la suivante : il existe dans le site catalytique de l'enzyme, deux acides aminés ionisables qui participent à la catalyse. Pour qu'il y ait catalyse, il faut que ces deux acides aminés se trouvent dans des états d'ionisations inversés : un protoné l'autre déprotoné. Ce modèle implique que l'enzyme existe sous trois formes, en ne considérant que ces deux acides aminés. Les charges ne sont pas représentées car les groupements ionisables peuvent aussi bien être des acides carboxyliques que des bases azotées protonées:
EH2: les deux acides aminés sont protonés
E : les deux acides aminés sont déprotonés
EH : un acide aminé est protoné, l'autre déprotoné
C'est dans la forme EH que les deux acides aminés se trouvent dans des états d'ionisations inversés : un protoné et l'autre déprotoné. C'est la forme active de l'enzyme. Le schéma réactionnel est le suivant :
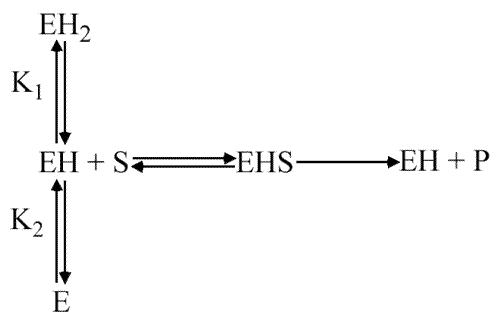
Seule la forme EH est capable de lier le substrat et de le transformer en produit. K1 et K2 sont les constantes d'acidité des chaines latérales des acides aminés impliqués dans la catalyse. En fait, expérimentalement, pour étudier le comportement catalytique d'une enzyme en fonction du pH, nous travaillons essentiellement avec une concentration saturante en substrat. On mesure donc un VM app: c'est un VM mais qui n'est qu' apparent,: c'est la vitesse la plus grande mesurable au pH considéré
Equations utilisées :
1. ( E )T = ( E ) + ( EH ) + ( EH2 )
2. K1 = ( EH ) ( H+ ) / ( EH2 )
3. K2 = ( E) ( H+ ) / ( EH )
4. VM = k2 ( E )T
cette valeur n'est en fait jamais atteinte puisque l'enzyme n'est jamais totalement sous sa forme EH: EH<( E )T
5. VMapp = k2 ( EH )
Résolution des Equations :
[2] ( EH2) = ( EH ) ( H+ ) / K1
[3] ( E) = ( EH ) K2 / ( H+ )
[1] ( E )T = { 1+[ ( H+ ) / K1] + [K2 / ( H+ ) ] } ( EH )
[6] VMapp = [ k2 ( E )T ] / { 1 + [ ( H+ ) / K1 ] + [ K2 / ( H+ ) ] }
soit:
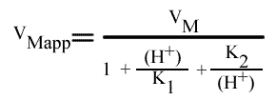
Que l'on peut exprimer aussi par: 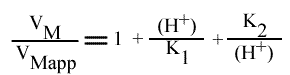
Afin de déterminer la valeur du pH optimum, nous devons regarder la courbe : le pH optimum de catalyse se trouve au sommet de la courbe : elle passe par un maximum donc sa dérivée première s’annule en ce point. Nous allons dériver l’expression ci dessus par rapport à la concentration en protons :
d(VM / VMapp ) / d ( H+ ) = ( 1 / K1 ) - [ K2 / ( H+ )² ] = 0
( H+ )² = K1K2
pHopt = ( pK1 + pK2 ) / 2
Exemple :
Pour avoir une idée, même approchée, de la nature des acides aminés impliqués dans la catalyse, dont la dissociation doit être inverse l'un de l'autre, il est intéressant de connaitre les valeurs des pK des chaînes latérales. Pour comprendre comment opérer, prenons des valeurs de pK1 et pK2 différentes.
Supposons que: pK1 = 6 et pK2 = 8
soit K1 = 10-6 M et K2 = 10-8 M
Donc: pHoptimum = ( pK1 + pK2 ) / 2 = 7
Nous allons envisager deux conditions extrêmes : le cas des pH très acides (où nous allons démontrer que la forme E est négligeable devant les autres formes) et le cas des pH très basiques (où c'est la forme EH2 qui est négligeable)
Aux pH très acides : pH < 6 donc ( H+ ) > 10-6 M; 10-5 M par exemple
K2 / ( H+ ) = 10-3
D'où : K2 / ( H+ ) << 1 et ( E- ) << ( EH )
( H+ ) / K1 = 10
D'où : ( H+ ) / K1 >> 1
A pH très acides, le rapport des vitesses s'écrit :
VM / VMapp = ( H + ) / K1
et: log VMapp = pH + log K1 + log VM
En traçant log ( VMapp ) = pH, on doit obtenir une droite de pente +1 et d'intercept = log K1VM
Avec un raisonnement similaire aux pH très basiques, nous trouverons l'équation :
log VMapp = - pH - log K2 + log VM
En traçant log ( VMapp ) = pH, on doit obtenir une droite de pente -1 et d'intercept = log VM / K2
En utilisant les des deux intercepts de ces droites ansi que l'équation générale au pH optimum, il est facile d'en déduire les valeurs individuelles de K1 et K2. Il faudra, par la suite, vérifier ces résultats en utilisant par exemple des réactifs covalants de ces acides aminés et voir si l'addition de ces réactifs, dans le milieu réactionnel, inhibe l'activité catalytique de l'enzyme.





