Le but de la théorie cinétique est de décrire les vitesses de réaction en fonction des propriétés physiques des molécules réagissantes.
Une approche théorique qui tient compte explicitement des structures des molécules réagissantes et de leur manière d'entrer en collision a été développée dans les années 1930 par Henri Eyring. Cette approche des processus réactionnels, connue sous le nom de Théorie de l'état de transition ou théorie de la vitesse absolue, constitue la base d'une grande partie de la cinétique moderne et à fourni une plate-forme extrêmement féconde pour comprendre comment les enzymes catalysent les réactions.
L'état de Transition
Considérons une réaction élémentaire bimoléculaire qui fait intervenir trois atomes, A, B et C : 
L'atome C doit s'approcher de la molécule diatomique A-B de sorte que, à un certain stade de la réaction, un complexe à potentiel énergétique élevé (donc instable), représenté par A--B--C se forme. Dans ce complexe, la liaison covalente A-B est sur le point d'être rompue alors que la liaison covalente B-C est sur le point d'être formée. Les distances interatomiques sont plus grandes dans le complexe que dans les états d'équilibre.
A--B--C est le complexe activé : le système est à son état de transition.
Méthode : Thermodynamique de l'état de Transition
Etant donné qu'une réaction ne peut se dérouler que si l'état de transition est atteint, on peut formuler une explication détaillée des mécanismes réactionnels.
Prenons le cas d'une réaction bimoléculaire qui se déroule selon le schéma suivant :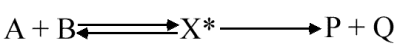
X* symbolise le complexe activé. De plus, compte tenu de la faible concentration du complexe activé, on présume que la décomposition du complexe activé est le facteur limitant de cette réaction.
Le diagramme d'état de transition ou diagramme du chemin réactionnel montre la variation de l'énergie potentielle du système au cours du trajet réactionnel.
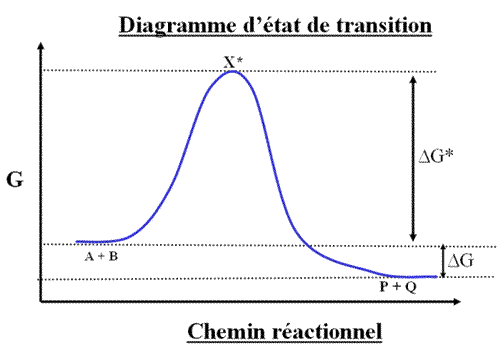
G est la variation d'enthalpie libre ( ou énergie libre de Gibb) entre l'état initial et l'état final.
En reprenant le schéma réactionnel, nous pouvons écrire :
d(P) / dt = d(Q) /dt = k (A) (B) = k* (X*)
k est la constante cinétique normale de la réaction élémentaire; k* est la constante de vitesse de la réaction de décomposition de X* en produits:
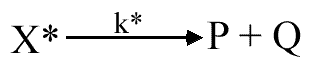
A l'inverse des molécules stables comme A et P, qui se trouvent dans un état énergétique minimum, le complexe activé est dans un état énergétique maximum et donc métastable (tout comme une balle en équilibre au bout d'une baguette). La théorie de l'état de transition prévoit néanmoins que X* est en équilibre rapide avec les substrats, c'est à dire :
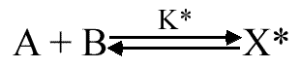 Equilibre entre les réactifs et X* | K* = (X*) / (A) (B) |
Ce postulat central de la théorie de l'état de transition permet d'appliquer les lois de la thermodynamique à la théorie des vitesses de réaction.
Si K* est une constante d'équilibre, on peut l'exprimer par :
- G* = - RT Ln K*
Où
G* est la variation d'énergie libre de Gibbs entre le complexe activé et les substrats.
En combinant ces équations :
K* = (X*) / (A) (B) = exp ( -
G* / RT)
X* = (A) (B) exp ( -
G* / RT)
d(P) / dt = k (A) (B) = k* (A) (B) exp (-
G* / RT)
k = k* expo( -G* / RT)
Cette équation indique que la vitesse de réaction dépend non seulement de la concentration de ses substrats mais qu'elle diminue de façon exponentielle avec G*.
Ainsi, plus la différence d'énergie libre de l'état de transition et celle des substrats est grande, moins l'état de transition est stable et plus lente sera la réaction.
Plus G* est faible et plus la cinétique sera rapide.
Il faut, maintenant calculer k*, la constante de vitesse de décomposition du complexe activé (souvent appelée la barrière d'activation ou encore la barrière cinétique de la réaction).
Ce modèle de l'état de transition nous le permet même si la dérivation qui suit n'est pas vraiment rigoureuse.
Le complexe activé est maintenu par une liaison dont on supposera qu'elle est si faible qu'elle volera en éclat dès sa première vibration. On exprime donc k* par :
k* = 
Où:
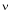- est la fréquence de vibration de la liaison qui est rompue lorsque le complexe activé se décompose pour donner les produits
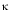- est le coefficient de transmission. C'est la probabilité pour que la décomposition du complexe activé X* se fasse bien dans le sens de la formation des produits plutôt que d'un retour aux substrats. Pour la plupart des réactions spontanées qui se font en solution, 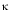est compris entre 0,5 et 1,0.
Il nous reste à déterminer la valeur de .
D'après la loi de Planck :
E = h donc = E / h
Dans ce cas :
E est la valeur moyenne de l'énergie de vibration qui conduit à la décomposition de X*
h est la constante de Planck (h = 6,6231 . 10 -34 J s-1 )
La mécanique statistique nous dit qu'à la température T, l'énergie normale d'un système oscillant est :
E = k B T
avec:
k B : constante de Bolztmann (kB = 1,3807 . 1023 J °K -1) et k B = R / N
k B T : représente essentiellement l'énergie thermique disponible.
k =
= E / h = k B T / h
Si on suppose, comme pour la plupart des réactions, que = 1 ( peut rarement être calculé avec certitude), l'expression de la constante de vitesse, k, pour notre réaction élémentaire est :
k = (k B T / h ) exp ( - G* / RT)
Cette équation indique que la vitesse de réaction diminue quand l'énergie libre d'activation , G*, augmente. Inversement, lorsque la température s'élève, ce qui augmente l'énergie thermique disponible pour amener le complexe réactionnel à un niveau énergétique supérieur à celui de la barrière d'activation, la réaction s'accélère. Bien sur, les enzymes étant des protéines, elles sont dénaturées par la chaleur ce qui explique que la vitesse d'une réaction enzymatique chute brutalement si l'on dépasse la température de dénaturation.
Un catalyseur diminue la valeur de deltaG*
La plus part des réactions observées dans le vivant sont lentes à réaliser in vitro, c'est à dire lorsque l'on met les substrats dans l'eau. On peut alors utiliser des composés qui accélèrent les réactions : ce sont des catalyseurs. Par définition, un catalyseur n'est pas transformé lors de la réaction. Il se retrouve intact à la fin de la réaction. Un catalyseur ne fait qu'accélérer la vitesse de la réaction qu'il catalyse. Un catalyseur abaisse la barrière d'activation de la réaction qu'il catalyse
Si un catalyseur abaisse la barrière d'activation d'une valeur
G*cat , alors la vitesse de la réaction est augmentée d'un facteur exp(
G*cat / R T ).
Ainsi une augmentation de la vitesse d'un facteur 10 demande un
G*cat = 5,71 KJ / mol , soit moitié moins d'énergie qu'une liaison hydrogène classique.
Fondamental : Une enzyme catalyse une réaction dans les deux sens
Remarquez que la barrière cinétique est abaissée de la même valeur pour les deux réactions : la réaction dans le sens de la formation du produit et la réaction inverse. Par conséquent, un catalyseur accélère d'un même facteur les deux réactions d'où une constante d'équilibre inchangée. L'enzyme n'est pas spécifique du sens dans lequel se fait la réaction.
Complément : Quelque fois, l'enzyme modifie le chemin réactionnel en introduisant des intermédiaires:
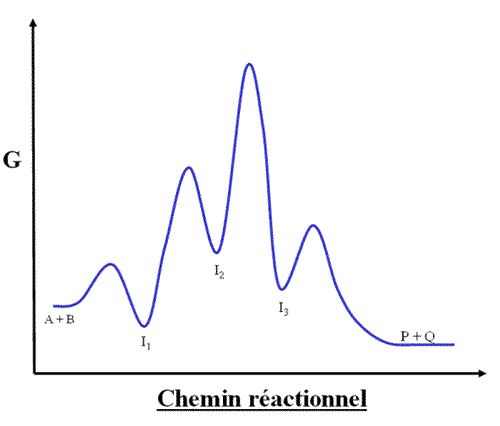
I1, I2 et I 3 sont des intermédiaires. L'étape déterminante est le passage de I2 à I 3 parce que c'est à ce niveau qu'il y a la plus grande différence d'énergie entre l'état initial et l'état de transition.
Effet de la température
La température joue sur les équilibres et sur les cinétiques.
En ce qui concerne les équilibres, il suffit de reprendre les expressionsde la théorie de l'état de transition mais en considérant maintenant une réaction réversible “classique”, le tout à l'équilibre :
- G° = - RT Ln K eq
Il suffit de rajouter :
- G° = H° - T S°
Avec:
- H° : enthalpie
et
S°: entropie
D'où :
Ln K eq = (-
H° / RT) + ( S° / R)
Puis de dériver cette expression par rapport à la température, on obtient ainsi :
d(Ln K eq ) / dT = (+ H° / RT2 ) . Equation de Van't Hoff
Expérimentalement, H° est obtenu en mesurant les K eq à différentes températures et en traçant - log K eq en fonction de 1 / T : on doit obtenir une droite de pente = - H° / R.
L'équation de Van't Hoff peut être utilisée pour déterminer les paramètres thermodynamiques de toutes les réactions équilibrées : les réactions impliquant des effecteurs linéaires , mais également la formation du complexe ES dans le cas d'un pré équilibre rapide.
A travers la théorie de l'état de transition, nous avions également démontré :
k = (kBT / h ) exp(-
G* / RT)
On pose : A = kB / h
k = A T exp (-
G* / RT)
Ln k = Ln A + Ln T – (
G* / R T )
- G* = H* - T S*
(
G* / R T ) = (H* / R T ) - (S* / R )
Et, en supposant que S* ne varie pas avec la température :
d(Ln k) / dT = (1 / T) + (
H* / RT 2) = ( H* + RT) / RT 2
On définit l’énergie d’activation, Ea : Ea = H* + RT
d(Ln k) / dT = Ea /RT 2
d( Ln k ) / d( 1 /T ) = - Ea / R . Equation d’Arrhenius
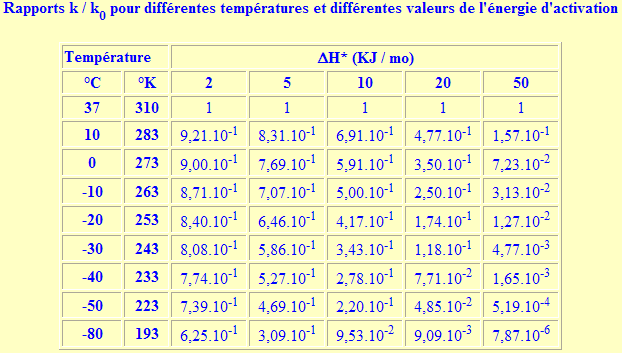
Les variations de la constantes de vitesse peuvent être très importantes à deux conditions: une valeur de H* grande et un écart de température important, comme le montre le tableau ci-dessous.
