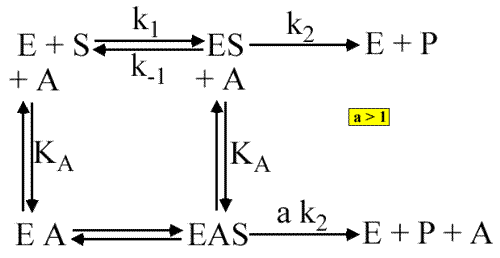
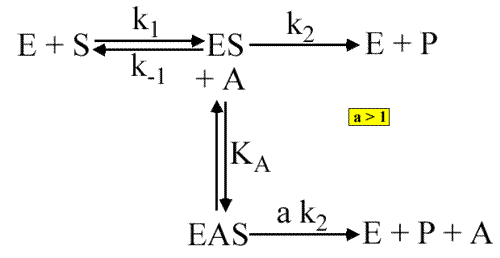
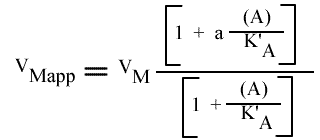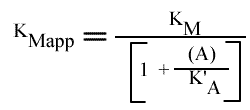Dans ce cas a >1 et très souvent a>>1. Le schéma général est :

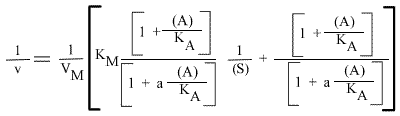
L'expression de la vitesse devient (en remplaçant F par A, puisqu'il s'agit d'un activateur) :
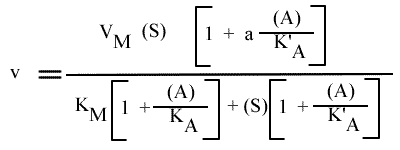
Dans laquelle VM est la vitesse maximale sans activateur.
Les expressions de la VMapp et KMapp sont:

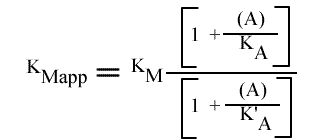
Et en double inverse:
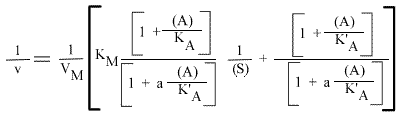
si bien que la représentation de Lineweaver Burk est linéaire.
Représentation de Lineweaver-Burk :
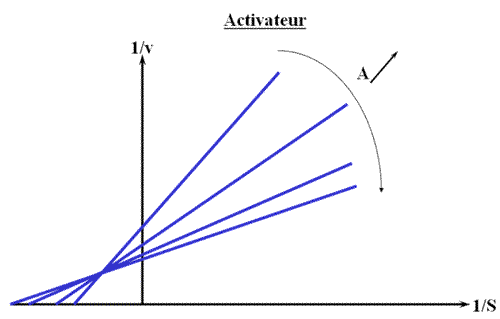
Conseil :
Regardez bien le sens de variation de la concentration en activateur, ce qui vous permet de distinguer l'activation de l'inhibition mixte (modèle d'une inhibition totale).
Les droites convergent en un point de coordonnées :

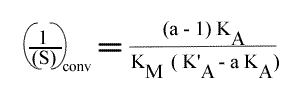
Remarque : Graphes secondaires:
Aucun des paramètres des droites ne sera linéarisable.
Méthode :
Pour arriver à extraire les constantes d'activation ainsi que a, il faut d'abord tracer les graphes VMapp et KMapp en fonction de ( A). Ces graphes ne sont pas linéaire.
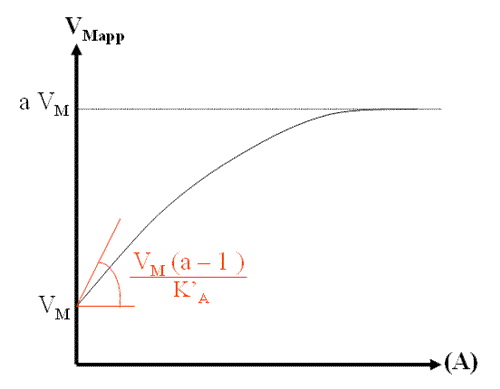
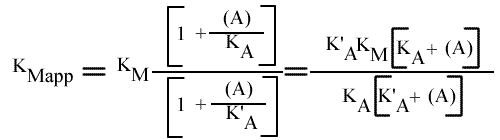
Il faut ensuite calculer les dérivées des fonction par rapport à (A);
avec d(u / v) = [ v.du - u.dv] / v 2.
Puis calculez la limite de ces dérivées lorsque (A) tend vers 0. C'est en fait la tangente à l'origine.
Puis il faut déterminer la limite de chaque fonction lorsque (A) tend vers l'infini: ici c'est l'asymptote à la courbe. Voici les résultats:
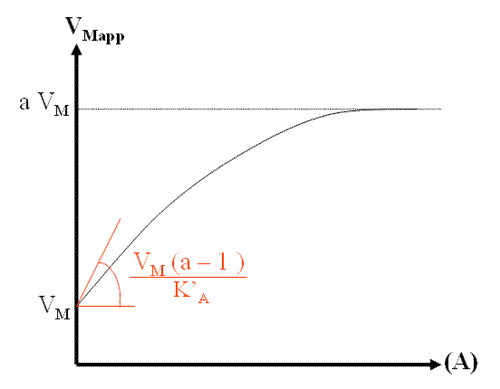
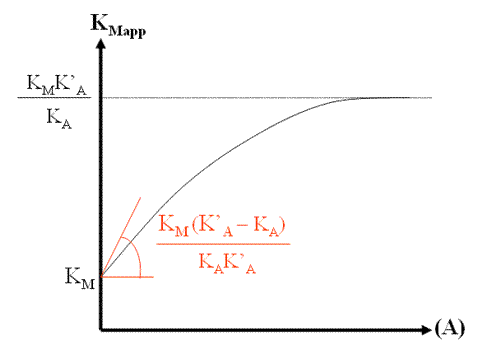
On peut de nouveau distinguer des cas limites.
Premier cas limite :
KA = K'A
Remarque :
Il s'agit d'une liaison indépendante des deux ligands sur leurs sites respectifs.
On a alors :

Remarque : Graphe de Lineweaver-Burk
Le graphe ressemble à celui que l'on obtenait avec une inhibition non compétitive sauf que l'ordre des différentes droites est inverse du précédent (1/v diminue quand (A) augmente).
Deuxième cas limite
KA est infini
Remarque :
Il s'agit d'un activateur conditionnel, qui ne se fixe que quand le substrat est déjà en place.
Dans ce cas :