Premier cas limite : a = 0
On suppose une inhibition complète où le complexe ESF n'est pas productif.
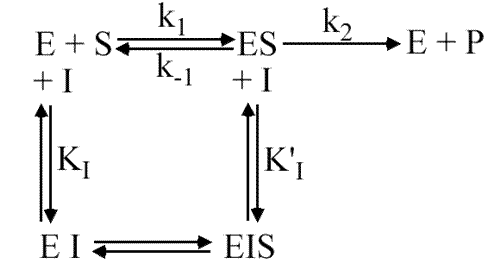
Cas général
Cas général: Inhibition mixte
KI et K'I différents de 0
La vitesse initiale de la réaction peut s'écrire sous la forme:
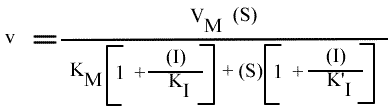
ou encore :

et, pour une représentation en double inverse, représentations de Lineweaver-Burk:
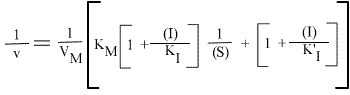
La représentation de Lineweaver Burk se compose de droites qui convergent en un point de coordonnées :

et
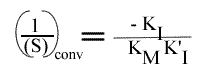
Représentation de Lineweaver-Burk :
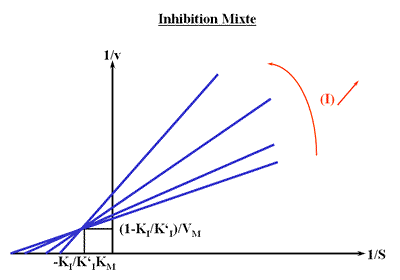
Remarque :
1 / (S)conv est toujours négatif alors que 1 / v conv est positif ou négatif selon le rapport des constantes d'inhibition.
Le point de convergence sera toujours situé à gauche de l'axe des ordonnées.
Pour caractériser complétement l'effecteur, il faut déterminer les deux constantes d'inhibition. Pour cela, il faut tracer un ou deux graphes secondaires.
Attention :
Le graphe 1 / v = f ( 1 / (S) ), (I) paramétrique est un graphe primaire.
Définition :
Un graphe primaire utilise directement les données expérimentales
Un graphe secondaire est tracé à partir de valeurs relevées sur un graphe primaire
Les points caractéristiques de chaque droite obtenue dans ce graphe sont:
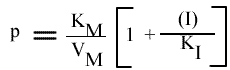
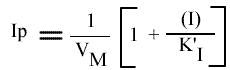
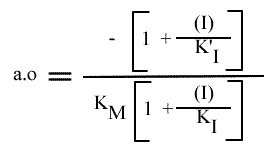
Remarque :
Les trois paramètres de la droite dépendent de la concentration en inhibiteur: le point de convergence sera donc bien situé en dehors des axes.
Ces paramètres peuvent être utilisés pour tracer un graphe secondaire.
Exemple :
Le tracé de l'Ip de chaque droite obtenue dans le graphe primaire, en fonction de (I) fournit l'un des graphes secondaires.
L'Ip peut s'écrire sous cette forme:
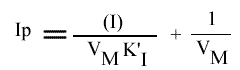
La représentation de l'Ip en fonction de la concentration en inhibiteur est une droite:

Remarque :
Les points caractéristiques de cette droite sont indicés d'un "s" pour bien souligner le fait qu'ils sont issus d'un graphe secondaire, ce qui évite ainsi de les confondre avec ceux du graphe primaire.
Le tracé de la pente des différentes droites du graphe primaire en fonction de ( I ) fournit un autre graphe secondaire que l'on exploite selon le même principe.
La représentation en est une droite dont l'intercepte donne KM /VM , la pente KM / VMKI et l'abscisse à l'origine est - KI.
Attention :
Le dernier graphe secondaire qui peut être obtenu est celui de l'a.o. = f ( (I) ). Mais l' expression de ce paramètre n'est pas linéarisable.
Cette technique permet :
De vérifier un modèle.
De minimiser l'erreur que l'on peut faire sur la détermination des grandeurs caractéristiques (VM, KM, KI, K'I...) en évitant de donner à une courbe (ou droite) un poids supérieur à celui des autres.
Complément :
Représentation de Dixon : 1 / v = f ( (I) ), (S) paramétrique.
C'est un graphe primaire.
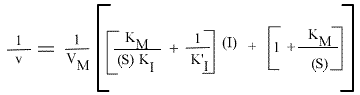
En traçant 1 / v = f ( (I) ), on obtient une droite par valeur de (S).
Toutes les droites convergent en un point
d'abscisse -KI
et d'ordonnée (1 / VM) . ( 1 - KI / K'I)
ce qui permet de déterminer KI et K'I.
Inhibition compétitive
KI est fini mais K'I tend vers l'infini
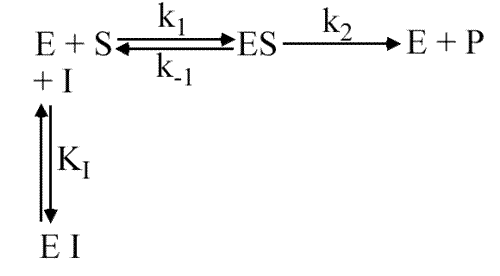
Cela signifie que le complexe ESI ne se forme pas: la liaison de I avec E est exclusive de la liaison de S avec E. Le site substrat est capable de fixer l'inhibiteur.
Remarque :
Dans ce modèle, l'enzyme ne possède qu'un seul site : le site catalytique.
Ce site peut être occupé soit par S soit par I
Pour un inhibiteur compétitif, on obtient :
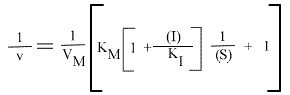
Seul le KM apparent est changé; la pente et l'a.o. dépendent de (I) mais pas l'intercepte. Les points caractéristiques des droites sont :
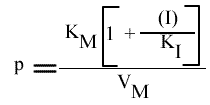
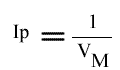
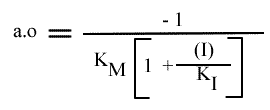
L'Ip est indépendant de la concentration en inhibiteur: le point de convergence se trouve donc sur l'axe des ordonnées.
Représentation de Lineweaver-Burk :

Méthode : Graphe secondaire
Le graphe où l'on porte la pente p de chaque droite obtenue dans le graphe primaire en fonction de (I) fournit KI facilement. Un deuxième graphe secondaire peut être obtenu en traçant l'inverse de l'a.o. en fonction de (I).
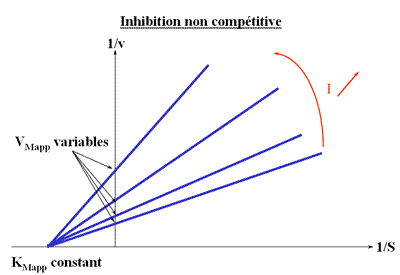
Inhibition non compétitive
KI = K'I
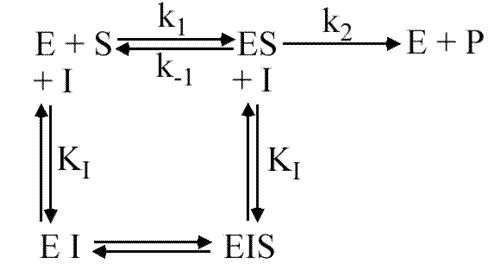
Il existe deux sites sur l'enzyme : le site catalytique et le site effecteur. Ces 2 sites sont indépendants c'est-à-dire que la liaison d'un composé sur son site ne modifie par l'affinité de l'autre site. En d'autre termes, l'effecteur se fixe de la même façon que le site catalytique soit occupé ou non par le substrat.
On trouve donc que les VM apparents sont seuls modifiés.
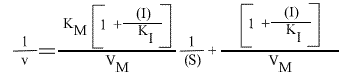
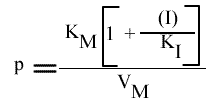
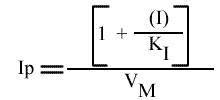
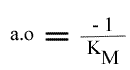
Les droites 1 / v = f (1 / (S) ) convergeront donc sur l'axe des abscisses puisque l'a.o. est indépendant de (I).
Représentation de Lineweaver-Burk :
Méthode : Graphes secondaires
Deux graphes secondaires peuvent être tracés: l'inverse de la pente ou l'inverse de l'intercepte en fonction de (I).
Inhibition in compétitive (ou conditionnelle)
K'I est fini et KI tend vers l'infini
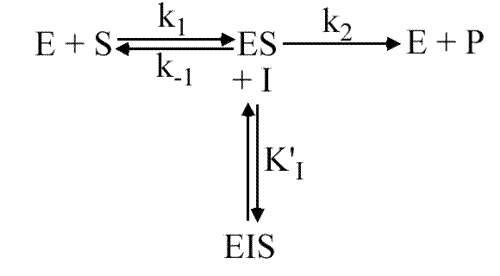
Remarque :
L'enzyme possède deux sites : le site catalytique et le site effecteur mais ce dernier n'est accessible qu'après liaison du substrat.
L'expression de l'inverse de la vitesse pour ce modèle est :
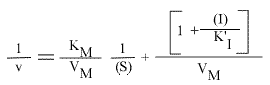
Les points caractéristiques des droites sont :
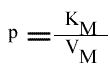
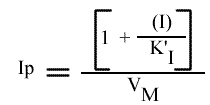
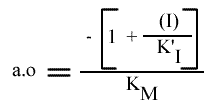
Remarque :
On voit que la pente est indépendante de (I), donc toutes les droites seront parallèles (convergence à l'infini).
Représentation de Lineweaver-Burk :
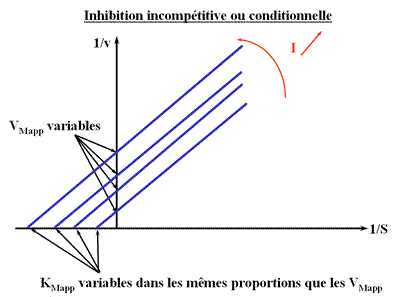
Méthode : Graphes secondaires
Le tracé de l'intercepte (Ip), de chaque droite obtenue dans le graphe primaire, pour une concentration de I donnée, en fonction de (I) donne facilement KI (autre nom de K'I dans ce cas).
L'a.o peut également être utilisée pour tracer un graphe secondaire.
Complément : Les différents types d'inhibition et la représentation Eadie-Hofstee:
Dans le cas où on utilise la représentation de Eadie-Hofstee, les formes des diagrammes en fonction du type d'inhibition sont:






