Document de cours
Modèle général d'un effecteur
Fondamental :
Un effecteur module la vitesse de réaction mais n'est pas indispensable, contrairement au substrat
On considère le cas où un composé F (dont on verra plus loin qu'il peut se comporter comme un inhibiteur ou comme un activateur) peut se fixer sur l'enzyme, en un seul site et qu'il modifie la vitesse de la réaction d'apparition des produits. On appelle ce composé un effecteur linéaire. Le schéma général est :
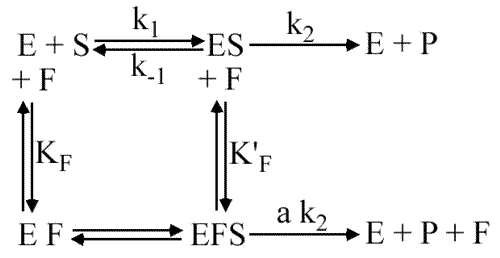
On pose que :
Les deux vitesses de formation du produit sont reliées par un facteur a (qui sera nul pour un inhibiteur total, supérieur à 1 pour un activateur, et compris entre 0 et 1 pour un inhibiteur partiel)
On travaille en excès d'effecteur: (F)>>(E)T, soit (F) = constante. Cela implique, aussi, que l'effecteur n'ait pas une affinité trop grande vis à vis de l'enzyme sinon toute celle-ci serait complexée par F. Si, au contraire, l'effecteur a une affinité pour l'enzyme de l'ordre de grandeur de la concentration de celle-ci, alors on parle d' inhibiteur puissant. Tout ce qui suit dans cette page ne s'applique pas à ce cas, et le traitement des résultats est donc sensiblement différent.
Les équilibres de fixation de F sur E sont toujours établis: ces réactions sont rapides et lors de la mesure de la cinétique, ils ont atteint leurs situations d'équilibre: on utilisera donc les constantes d'équilibre et non les constantes de vitesse dans toutes les réactions impliquant l'effecteur F. Mais il est facile de vérifier que si l'on ne fait pas cette hypothèse, on obtient le même résultat.
Un effecteur : F, Modèle général
Équations utilisées :
(E)T = (E) + (ES) + (EF) + (ESF)
d(ES) / dt = k1 (E) (S) - ( k-1 + k2 ) (ES) = 0
KF = (E) (F) / (EF)
K'F = (ES) (F) / (ESF)
v = k2 (ES) + a k2 (ESF)
VM = k2 (E)T
Remarque :
Ici, on pose que la vitesse maximale est VM = k2.(E)T , c'est-à-dire la vitesse maximale de la réaction sans effecteur. Il est évident que cette vitesse pourra être dépassée en présence d'un activateur
Résolution :
[2]: KM = (E) (S) / (ES) = ( k-1 + k2) / k1
(E) = (ES) KM / (S)
[3]: (EF) = (E) (F) / KF = [ KM / (S)] [ (F) / KF ] (ES)
[4]: (ESF) = (ES) (F) / K'F
[1]: (E)T = { 1 + [KM / (S)] [ 1 + ( (F) / KF )] + [ (F) / K'F ] (ES)
[5]: v = k2 (ES) + a k2 [ (F) / K'F ] (ES) = [ 1 + a [ (F) / K'F ] ] k2 (ES)
v = { [ 1 + a [ (F) / K'F ] ] VM (S) } / { [ KM [ 1 + ( (F) / KF )] ] + [ (S) [ 1 + ( (F) / K'F ) ] }
v= VM (S) (1 + a (F) / K'F ) / [ KM ( 1 + (F) / KF ) + (S) ( 1 + (F) / K'F ) ]
Que l'on peut aussi écrire sous la forme
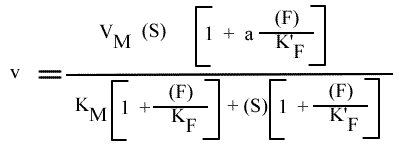
ou
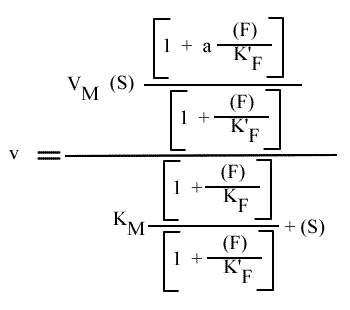
et, pour une représentation en double inverse:
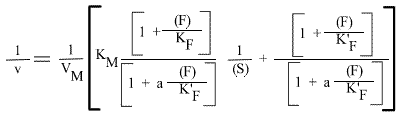
Les représentations de Lineweaver-Burk or Eadie-Hofstee sont donc des droites pour F paramétrique. La vitesse maximale apparente, VMapp et le KM apparent sont donnés par :
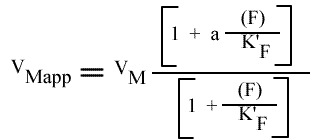
et
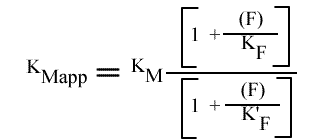
Dans une représentation de Lineweaver-Burk, les droites convergent en un point de coordonnées :
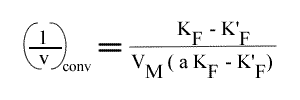

qui peut être situé n'importe où dans le graphe.





